 Chapter 1: Intro to Lartravera
Chapter 1: Intro to Lartravera
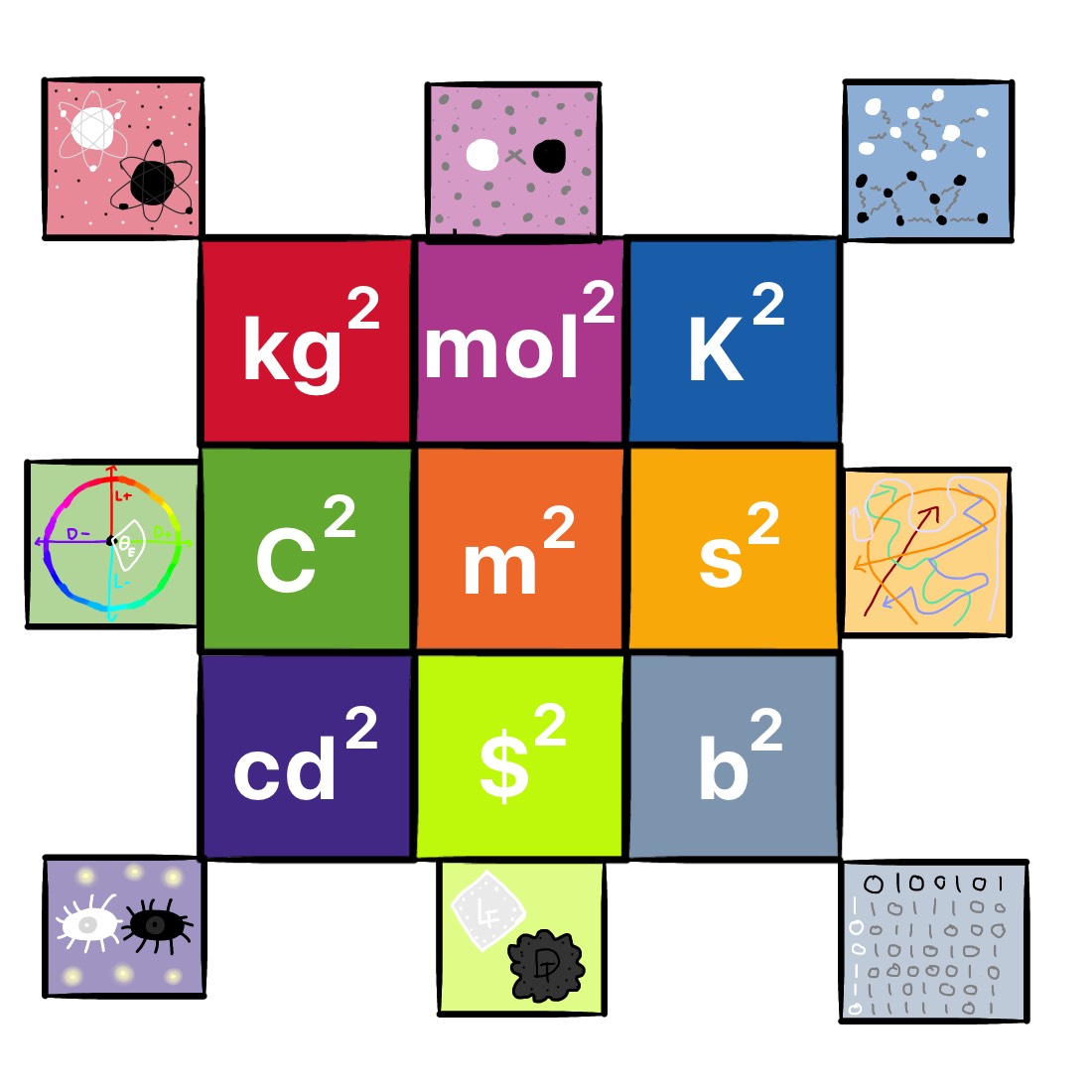
In our world's standard system of measurement,
time is measured in seconds (s),
distance is measured in meters (m),
mass is measured in kilograms (kg),
temperature is measured in Kelvin (K),
electric current is measured in amperes (A),
amount of atoms is measured in moles (mol),
visible light intensity (at a single point) is measured in candelas (cd),
currency has many measures but the most common currency name is the dollar ($), and
information's actual base measurement is the bit (b).
The first seven of these are the base units of the metric system, and the latter two are units I feel are similarly fundamental.
But what about squared units? In our world, square meters (m2) are a unit of area, but what would
a "squared second (s2)" describe? What about a "squared kilogram (kg2)"? In our world,
these square units don't have a good meaning... but I've been looking into an alternate universe where they do.
Imagine a universe different from our own, one in which the beginnings of matter itself played out in a very different way.
In our world, two types of matter existed at the universe's beginning: matter and antimatter.
The two annihilated with each other, and once the dust settled only matter remained. In this alternate universe,
there were also two types of matter, but rather than annihilate with each other, the two kinds of matter came together,
becoming reliant on each other rather than destroying each other, and it was with both of these kinds of matter that this universe was shaped
and populated. The beings who live in this universe have languages that express this duality far better than any of our tongues, but for our purposes
we shall call these forms of matter "littra" and "darra", distorted forms of "light matter" and "dark matter"
(but these matters are not related to the dark matter that holds galaxies together in our world, these are just the names I've chosen to use).
We also need a name for this universe, and for that we will combine the words for these types of matter and the word "universe": Lartravera.
In Lartravera, each of the nine units I gave above has a meaning when squared... so what does each one mean?
Matter and Mass (kg2)
In our world, the concept of mass and the concept of amount of substance are equivalent, but that is not true in Lartravera.
Neither littra nor darra have mass intrinsic to themselves, but littra and darra do give mass to each other.
If the amounts of littra and darra that comprise an object can be measured in kg, then the actual mass could be measured in kg2,
as doubling the amount of littra in an object or doubling the amount of darra in an object will always double the object's mass;
in other words, an object's true mass is the product of the amount of littra that it's made of and the amount of darra that it's made of.
For an example, an object comprised of 50 kg of littra and 22 kg of darra would have a mass of 1,100 kg2.
Remember, in Lartravera kg would just be a unit of amount of matter of one type, while kg2 would be a unit of mass.
In theory, this means pure littra and pure darra would always have masses of 0 kg2, but as you might have already guessed,
pure littra and pure darra do not exist macroscopically; even if a material made of pure littra or darra did exist,
some atoms of the other kind of matter would fuse into the material from its surroundings. Scientists in Lartravera have attempted to isolate
littra and darra from each other in the lab, and though some have come very close, none have quite been successful. Creating pure littra or
pure darra at a macroscopic scale in Lartravera would be a similar feat to creating a temperature of absolute zero in our universe.
Gressa Atoms (mol2)
It's undeniable that the masses of littra and darra come from each other, but how exactly does this work?
All sorts of theories have been posed on the quantum interactions that create mass in Lartravera, but the prevailing consensus is that in any object,
littra and darra's interactions with each other create a third type of matter, "gressa". Calling gressa a form of matter is a bit misleading,
though, as it's more of a quantum phenomenon than an actual type of matter: gressa only exists in conjunction with littra and darra,
and if an object loses some of its littra and/or darra, some of that object's gressa stops existing.
Though atoms of littra and darra are still made of subatomic particles of that type of matter, the quantum interactions that cause the existence of
gressa occur at the atomic level. Each and every atom of littra creates one atom of gressa with each and every atom of darra,
which means that the amount of gressa atoms in an object is equal to the product of the amount of littra atoms in that object
and the amount of darra atoms in that object. This makes the mole a more useful unit than in our world, but regular moles only measure
littra and darra, as gressa is better measured in mol2. The theory of how this ties into mass is that littra and darra don't have mass
at all, it's the gressa that has mass, but since gressa only exists in union of the two real types of matter,
theories of how Lartraveran physics works can still make sense with an alternate theory of mass that does not incorporate gressa.
Two-Matter Temperature (K2)
The temperature of the littra in an object and the temperature of the darra in an object are scientifically independent values
that could be measured in K, but living beings in Lartravera generally don't feel these temperatures separately.
The kind of temperature living beings feel, whether in the environment or in objects or in themselves is generally based on
the product of the temperatures of the two types of matter making up whatever object or surroundings the temperature refers to,
and thus that kind of temperature could be measured in K2. Since such squared temperature is prone to much greater fluctuation
than one-dimensional temperatures, living beings in Lartravera have generally evolved to withstand a much larger range of temperatures
than us humans have, but spreading to new lands is often harder for lifeforms in Lartravera than it is for lifeforms in our universe
since the temperature can get so much more out of the habitable ranges of those lifeforms than it can here.
Two-Matter Electric Charge (A2)
The types of subatomic particles and atoms themselves are the same for both littra and darra, but although atoms
only consist of particles of one type of matter, molecules always contain atoms of both types of matter,
and the unique interactions between the electron equivalents of the two types of matter result in all sorts of interesting molecules
that have no equivalents at all in our universe. This is especially true because littra and darra have separate types of electric charge
as a natural consequence of having different equivalents of electrons and protons, thus electricity is also a two-dimensional quantity in Lartravera.
Electric charges and currents of one type of matter could still be measured in coulombs and amperes, but some electrical phenomena and devices
on the macrocosmic scale occur/work with both types of charge, thus the units of C2 and A2 also make sense when talking about
electricity on a more general scale...
Planar Time (s2)
...wait, if an ampere is a coulomb/second, wouldn't a squared ampere be a squared coulomb/squared second?
Well, as it turns out, even time itself isn't the same in Lartravera as it is in our universe. Time only has one dimension in our universe,
but it has two in Lartravera. In simple terms, one axis of time represents causality while the other represents possibility,
but of course in reality there's no "axes" and all directions of time have some element of both. Going back to the simpler model,
moving forward on the causality axis would be similar to moving forward in time in our world, while moving forward on the possibility axis
would be like going through the same point in the kind of time we're used to but getting farther and farther from what originally happened
as minor changes to events pile up. In Lartravera, inanimate objects tend to exist in a pretty standard fashion across this 2D plane of time,
but the paths living beings take through time are fascinating. Rather than only feeling a single point of time, living consciousnesses
tend to experience a small area of time, such as 1 s2, at once: not enough to cause significant discomfort most of the time,
but enough for people to feel a little bit of foresight and recollection throughout their lives, and when that 1 s2 contains a sudden
change (such as a car crash) they might have a short "temporal headache" from experiencing a split-second before the change and a split-second
after the change at once. The paths that lifeforms take through time aren't always linear: sometimes they zig-zag,
sometimes they speed up and slow down, sometimes they reverse direction, sometimes they cross the same point in time multiple times, and so on.
Though the path a lifeform takes through time is always continuous, its direction can change suddenly, and the actions taken by that lifeform
may be able to affect their path through time, at least slightly. The bodies of lifeforms still age and de-age in linear time,
but their memories and experiences operate on this planar time. In Lartravera, lifeforms find friends and family in other lifeforms that are
traveling on the same path through the plane of time as themselves, while those on different paths through time meet momentarily
and then diverge from each other, with the versions of each other in their paths being less like people and more like parts of events.
When it comes to measuring time, linear time could be measured in seconds and would be used to describe the passage of causality,
travel along possibility, the way time affects inanimate objects, and the physical ages of lifeforms, while planar time could be measured in
squared seconds and would mostly be used to describe phenomena relating to lifeforms' experience through time, such as their mental ages
and the rates and patterns by which their path through the plane of time operates.
This concept of planar time is why the squared ampere is useful, as Lartravera contains advanced,
intelligent civilizations that understand time and consciousness better than we do, and these civilizations have created devices
that can be tied to a lifeform's path through time to ensure it travels through the plane of time along the same path as the lifeform.
Thus, while the unit A2*s (C2/s) can be used to measure two-matter electrical current through linear time,
the unit A2 (C2/s2) can be used to measure the two-matter electrical current through planar time
displayed by these life-tied devices.
Di-Photonic Visual Receptors (cd2)
Unlike just about everything else in Lartravera, photons do not come in two varieties:
there's no littra light and darra light, it's just light. What is different, however, is the way lifeforms perceive it.
Lifeforms in Lartravera that have the ability to see photons usually have an even number of visual receptors,
half of which are tuned towards littra and half of which are tuned towards darra.
The visible spectrum of light for the littra "eye" and the visible spectrum of light for the darra "eye" are often separate parts of the
light spectrum, thus there are two ranges of light that a lifeform will see, one range with their littra-based visual receptors
and one range with their darra-based visual receptors. However, since littra and darra depend on each other so heavily,
these visual receptors can't really perceive the photons in their range without help from the other receptor(s),
which of course require photons of their own range. The amount of light a lifeform actually sees is based on the product of the littra-range light
that hits their visual receptors and the darra-range light that hits their visual receptors,
so while the candela would be used to describe the visible light of one range coming out of a light-emitting point,
the actual visible light seen is the product of the two spectrums and would thus be more appropriately measured in square candelas.
Skreeeeeeena's Two Currencies ($2)
The concept of currency, and indeed possessions at all, isn't quite as applicable in a world with diverging time paths
as it is in ours, but some civilizations in Lartravera still have currencies. For a specific interesting example,
we will turn to the currency system of the country Skreeeeeeena, which is on a pretty remote planet.
This country's lifeforms have not made contact with any lifeforms from planets other than their own, so as far as they know
they're alone in the universe (though, as we know, they definitely aren't). Thanks to the diverging paths in time,
the general populous of Skreeeeeeena values self-sufficiency more than we do, but there's still a currency because the country's government
still wants its people to be dependent on society and thus willing to obey its laws. As a compromise between these mentalities,
rather than just having one currency, Skreeeeeeena has two currencies: liratars (l$) and dalatars (d$). As their names imply,
liratars are minted with metals that are mostly made of littra, while dalatars are minted with metals that are mostly made of darra,
but that's not really important. What is important is the way they're earned: jobs that require more physical work
(farming, factory work, blacksmithing, etc) pay in liratars, while jobs that require more mental work
(such as those in business, science, or teaching) pay in dalatars (jobs that are especially taxing in both of those areas pay both,
as do high-level governmental jobs because of course the government is going to give itself unfair advantages). Though a select few items,
such as the tools required to do a job themselves, only cost one currency, most purchases in Skreeeeeeena cost $2,
which is the product of l$ and d$. For example, if something costs 3,600 $2, then you could pay for it with 60 l$ and 60 d$,
or with 40 l$ and 90 d$, or with 200 l$ and 18 d$, or 1 l$ and 3,600 d$, or even 360,000 l$ and 0.01 l$.
This system forces most citizens of Skreeeeeeena to have two jobs, one that pays liratars and one that pays dalatars,
as they need some of both to buy almost anything, and for the most efficient purchases they'd want to spend equal amounts of liratars and dalatars,
but of course many of these lifeforms have higher-paying jobs in one currency than the other...
Grey Bits (b2)
Even the nature of information is different in Lartravera than in our universe.
Thanks to interactions betwen the two-matter system and planar time that I don't fully understand yet,
a phenomenon similar to the theory of gressa atoms occurs with bits of information: if you have bits of information on the littra of a system
and bits of information on the darra of system, you can use known facts about the two matters and about planar time to derive additional information
about the system, information that I like to call "grey bits". Similarly to gressa atoms, each and every littra bit creates a grey bit
with each and every darra bit; this means that while the amount of information on one matter type still should be measured in bits,
the unit of squared bits could be used to measure grey bits, especially in a probabilistic context rather than in a computing context.
Not only can grey bits be measured as additional information, but by taking advantage of movements along the possibility directions of time,
grey bits can even be altered and manipulated even though they're not "real" bits. Advanced computers and artificial intelligences in Lartravera
use this property of information to massively increase their storage space, RAM, and other aspects via encoding bits onto littra and darra
in equal amounts to maximize the amount of grey bits that they have to work with, then they exclusively manipulate the grey bits
while leaving the real ones unaltered (manipulating grey bits can be done without affecting the real bits, but doing anything to the real bits
will cascade changes through many of the grey bits): for example, if a computer has 1 Gb encoded in littra and 1 Gb encoded in darra,
then it would have 1 Gb2 of grey bits. Since bits are a finite object in a computer, using squared bits as a unit in a computing context
is redundant as you can just measure in regular bits, and in this case 1 Gb2 equals a whopping 1 Eb of grey bits.
Grey bits are pretty unreliable for computer design unless you're an expert because they're quite vulnerable to both small changes in the real bits
and in alterations to their path through planar time, so these computers tend to use much of their grey bit storage space on duplicates of
the same grey bits, so that when the active grey bits are altered in an unintended way they can simply overwrite them with the backup.
Still, even if only a thousandth of the grey bits are actually used, this style of computer storage is still far more efficient than
anything we can do in our world, though it is more prone to errors than our own computers.
Space is still 3D (m2, m3)
Despite all the differences between Lartravera and our universe, distance and space itself are the same in both universes.
Sure, the contents of space and some of its properties are massively altered thanks to the two types of matter, planar time, and so on,
but the fundamentals of space are the same, and this includes the amount of dimensions: space in Lartravera is also three-dimensional,
so m2 and m3 would still measure area and volume. The fact that space is three-dimensional when almost everything else
in Lartravera is embedded in duality has caused no shortage of flummoxing to scientists across Lartravera, and the common consensus among scientists
in many civilizations is that there must be an unseen fourth dimension of space that reestablishes duality; no scientist has evidence of such a
fourth dimension, but in many civilizations in Lartravera scientists that do not subscribe to this belief are shunned,
as to those who inhabit Lartravera, duality is the principle by which the universe operates.
In explaining all this, I've made many oversimplifications and changed around names and ideas to help with
understanding the principles behind the differences between our universe and Lartravera at the most fundamental level.
For one thing, the many civilizations across Lartravera have come up with many different systems of measurement,
each with their own units and terminology. Though squared units can be used for the measures I've described,
most Lartraveran civilizations have come up with measuring systems that, for example, have entirely separate units for "amount of matter" and "mass"
rather than measuring mass by the square of the matter unit, acknowledging the product rules but not defining their units around them.
It's also true that the nine base units I chose to use here aren't the only possible base units, and indeed many Lartraveran measuring systems
have a different set of base units than our world's SI. Beyond all that, so far I've mostly examined Lartravera from the perspective of the laws of physics
and how the squares of our base units relate to them, but there's so much more to say about this universe and the way it's formed and developed
as a result of these differences...
 Chapter 2: Mechanical Units
Chapter 2: Mechanical Units
When I first began researching Lartravera, I was satisfied with looking at just the nine squared base units.
However, the point of base units is that they can be multiplied and divided to get all sorts of derived units,
and it's these derived units that really make the measurement system complete. So what derived units would be used in Lartravera?
Velocity and Acceleration
Velocity and acceleration make much more sense from a linear time perspective than a planar time perspective,
as the velocity of an object tends to be much more predictable when only considering movement along the causality axis than when
moving along some other axes of time. That being said, since the causality/probability axis model is a simplification, lifeforms that
are moving on a certain axis of time can exert forces on objects to stabilize their movements towards their axis of time to an extent,
so there are situations where velocity and/or acceleration in planar time are units that can be used,
at least if you're using a theory of Lartraveran physics that assumes that all objects occupy a small area of time at once like consciousnesses do
rather than only existing at a single point at once or existing on an entire line of the plane at once.
Linear-time velocity and acceleration could be measured in m/s and m/s2 respectively, while planar-time velocity
and acceleration could be measured in m/s2 and m/s4 respectively...
...wait, the units for linear-time acceleration and planar-time velocity are the same?
There's a theory about this: according to Delisha's Hypothesis, the default path through time of all
non-living objects moving at a constant linear-time acceleration (such as an object in freefall) is a zig-zag path through time that has its
bottom corner at the point where the object's motion began. If an object is moving at a constant planar-time velocity,
and the zig-zag path means its rate of travel through linear time slows down at a rate directly proportional to planar time
(I guess that ratio would be measured in s/s2 = Hz), that means that constant planar-time velocity and constant linear-time acceleration
are actually the same thing! There's also Colinnnniss's Collorary, which builds on this by defining the ways in which objects' paths through
planar time are distorted by other kinds of non-constant motion, and these paths make it so planar-time acceleration is equal to linear-time snap
(m/s4), planar-time jerk is equal to linear-time m/s6, and so on.
That being said, these theories don't really line up with how planar time has been observed to behave, as the paths living beings take through
planar time are measurable to square days in their mental future with fair accuracy for species that live long enough
(and keep in mind that (in the time units of our world) one square day equals 576 square hours, which equals 2,073,600 square minutes,
which equals over 7 billion square seconds), and so a theorem that supposes a change in an object's time path being so dependent on motion
goes against the standard understanding of time. After all, in the usual understanding of Lartraveran time, only consciousnesses have actual paths
through time, while objects just exist in different states in different areas of time rather than really moving through it.
Density
Density comes in two forms. Density of matter, i.e. how tightly the littra and darra in an object are packed together,
could be measured in kg/m3, while the mass density we're familiar with would be measured in kg2/m3.
If you divide mass density by matter density, you get mass-matter ratio, measured in kg2/kg (which I guess just equates to kg),
which sort of measures how much more mass there is than matter. For example, an object with 30 kg of littra and 10 kg of darra in it would have a
total matter amount of 40 kg, a mass of 300 kg2, and therefore a mass-matter ratio of 7.5 kg2/kg. On the other hand,
an object with 20 kg of each of the two matters would still have 40 kg of matter but would have 400 kg2 of mass, and thus its
mass-matter ratio would be 10 kg2/kg. In general, the maximum possible mass-matter ratio for a certain amount of matter is 0.25p,
where p is the amount of matter, as the amount of mass you'd get with that amount of matter evenly split between littra and darra is
0.25p2. Some solid objects in Lartravera have the property of "grey hollowness", where the object has mass spread throughout it
but does not actually have any matter too far from its edge, which supports gressa theory
(i.e. the littra and darra inhabit the edge of the object while the gressa exists in the interior). Objects that exhibit grey hollowness can thus
have their matter density measured via surface area instead of volume, so matter density would be kg/m2 while mass density would
still be kg2/m3. Taking mass density and dividing it by this surface area matter density gives you a unit that could be
measured in kg/m, which sort of represents how spread apart the matter in an grey hollowness-exhibiting object is.
Space of Possibilities
There's a very important concept in Lartraveran physics that doesn't really have a useful equivalent in our world.
Since lifeforms exist at many points in time at once, any lifeform that's not standing perfectly still, which is pretty much every lifeform ever,
also occupies multiple points in space at once from their perspective. This doesn't just apply to lifeforms,
as if you look at all the positions of a single object over a given area of time, it also occupies multiple points in space over that area of time,
even if the "object" in question is treated as if it has no size and only exists at a single point in space per single point of time.
We can measure the total volume an object exists in across a set area of time in the typical volume unit of cubic meters,
which in this case refers to "volume of possibilities". The unit I mentioned earlier that's uniquely Lartraveran is m3/s2,
which measures "space of possibilities", the amount of volume in space an object exists in per unit of planar time.
This unit can be used on several ways: the most obvious is as an average (if an object's volume of possibilities over a given time area of
5 s2 is 20 m3, then its average space of possibilities over that interval is 4 m3/s2), but if we can
define velocities and accelerations at single instants in time then we can do the same for space of possibilities
(saying that an object has a space of possibilities of 4 m3/s2 at a single point in time makes as much sense as saying
that an object has a velocity of 4 m/s at a single point in time, and as you'll soon see, instantaneous space of possibility shows up in quite a few
places in Lartraveran physics) by defining it as a rate of change. For example, let's consider a hypothetical object that always occupies
10 m3 in 1 s2, but it's volume of possibilities only changes by 5 m3/s2 because half of the volume
it occupies in one squared second is still occupied by it in the next squared second. This object's average space of possibilities
is 10 m3/s2 when measuring 1 s2, but decreases to 7.5 m3/s2 for a 2 s2
interval and decreases further (approaching but never reaching 5 m3/s2) as the area of time we're averaging over increases,
while its instantaneous space of possibilities, i.e. its space of possibilities as a rate of
change, is 5 m3/s2. Though average space of possibilities is important for lifeforms,
instantaneous space of possibilities is seen more often in the equations that detail the laws of Lartraveran physics, so when I refer to
space of possibilities from this point on, I'm referring to instantaneous space of possibilities.
Forces
In Lartraveran physics, force is not the product of mass and acceleration. Instead, force is defined by the fact that
applying a force to an object causes change in its space of possibilities. Space of possibilities as a rate of change naturally occurs on its own,
so forces cause an increase or decrease in that rate. A unit of Lartraveran force can be defined as "a force that causes the space of possibilities
of a mass of 1 kg2 to increase its rate of increase at a rate of 1 (m3/s2)/s2", so the unit here
would be kg2*m3/s4, a unit which I'll call the Neotow (No). Whereas force in our world is directional (so
using positives and negatives to describe it depends on frame of reference), Lartraveran force has both direction and sign.
Repulsive forces (pushes) are positive because they expand the space of possibilities, while attractive forces (pulls) are negative because
they decrease the space of possibilities. All forces in Lartravera are repulsive or attractive. For example, gravity is an attractive force,
while forces caused by collisions (such as when you push an object with your hand) are often repulsive.
Forces between matter rather than mass do exist as well, and those could be measured in kg*m3/s4 = No/kg,
but matter forces have much weaker effects than mass forces because objects have exponentially
(actually quadratically, not exponentially, but you get the idea) more atoms of gressa than they have atoms of
littra and darra, so on the macroscopic level they can generally be neglected. In our world, macroscopic forces can be explained by the sums
of the force's effects on individual particles, but this is not always true in Lartravera: for example, because objects have mass as a whole
rather than the individual atoms having their own masses, mass forces tend to apply specifically to objects as a whole,
not to each of their tiny parts. Because a constant force causes space of possibilities to increase at a constant rate,
while space is 3D and so velocity is generally proportional to the cube root of space of possibilities, a force's effect on the actual motion
of an object is reduced on objects that already have a large space of possibilities.
This in turn means that repulsive forces (which increase space of possibilities) have their effect on the motion of an object weaken over time,
while attractive forces (which decrease space of possibilities) have their effect on the motion of an object strengthen over time,
but since repulsive forces cause objects to get farther from one another while attractive forces cause objects to get closer to one another,
this behavior is what we'd expect forces to do anyways. As far as I've seen, there's no one unit for the effect force has on motion:
since force is defined over planar time, forces' effects on linear-time motion depend on the path through time being used as the frame of reference,
as well as the space of possibilities of the object the force is being exerted on. "Linear-time force", measured in
kg2*m3/s3 = No/s, could be used to measure how much a force applies over a particular time path, but changes in
space of possibilities are best measured over planar time, so using linear-time force doesn't give you the whole picture of what a force is doing.
Admittedly, my analysis on how force works in Lartravera wasn't perfect, so I may have gotten some of this incorrect.
Momentum
Momentum is much simpler than force in Lartravera. Momentum laws deal with collisions, which are events that happen at
points in time, thus the planar time stuff doesn't come into play, so momentum is still just the product of mass and linear-time velocity,
which in Lartravera means it could be measured in kg2*m/s. In our world, dividing momentum by force just gives time,
so the amount of momentum increase by a given force is based purely on how long the force is applied for,
but in Lartravera dividing momentum by force gives a unit of s3/m2, which I believe in this case refers to
linear time multiplied by distance then divided by space of possibilities, so when a given force is applied to an object, the momentum it gives
it is increased for an object with a small space of possibilities (this checks out with the way force works) and increases as the force is
applied across a larger distance and a longer linear time across the path of time being analyzed...
or maybe I'm reading these numbers wrong. Of course, a repulsive force's increase on momentum slows down over time:
as the space of possibilities increases, the force's effect on velocity and momentum decreases.
An attractive force would cause a greater change in momentum over time as the space of possibilities decreases,
but eventually this will break down, either from the object reaching the source of the attractive force
and the counteracting pushback force and momentum change from the collision canceling things out, or from the attractive force naturally lowering
as the space of possibilities of the object getting too small, as an object's space of possibilities can never be zero.
Energy
Though gressa atoms are what give objects mass in the gressa theory of Lartraveran physics, gressa does not have any energy,
only littra and darra do. Energy is also intrinsically tied to space of possibilities, as an object with a larger space of possibilities in
Lartravera naturally has more energy. However, energy is only proportional to the square root of space of possibilities, so an object with the
same amount of matter and quadruple the space of possibilities will have double the energy. This means that the unit kg*m1.5/s can
be used to measure energy in Lartravera, a unit that I'll be calling the Kristine (Ki). In our world, the amount of energy gained per force
is just equal to distance it's pushed, but in Lartravera dividing energy by force gets you a unit with dimensions of Ki/No or
s3/m1.5/kg; if I'm reading these numbers right, this means (planar time)/sqrt(space of possibilities)/(mass-matter ratio),
so this means that the energy given to an object by a repulsive force is proportional to the planar time the force acts over,
inversely proportional to the square root of the average space of possibilities over the time the force is being applied, and inversely
proportional to the mass-matter ratio of the object... or, again, maybe I'm reading these numbers wrong. Power (the rate of output of energy)
is still energy over linear time as expected, so the unit for that could be Ki/s (kg*m1.5/s2), a unit called the peos (P),
though in the case of an electric device that's tied to its owner's path through time, the power being exerted by that device could be measured
in Ki/s2 (kg*m1.5/s3) since it's generating energy over planar time rather than linear time.
Also, keep in mind that in the case of linear power, the variability of direction through time means that from the perspective of a consciousness,
the output of energy could easily appear to reverse, and thus the measurement of linear power
could be measured as negative if its previous measurement was ruled to be positive.
Indeed, the fact that time does not have a single direction in Lartravera means that all processes in Lartravera are reversible,
so concepts like an "arrow of time" and entropy are either subjective or outright nonexistent.
Pressure
Pressure can still be defined as force per surface area, which in Lartravera could be measured in No/m2, but the
curious fact about pressure is that it would almost always be a negative value when measured this way, as pressure generally keeps things
held together, thus it's attractive, so the Neotow measure of the force in question is negative. This also means that pressure generally causes
a loss of energy: the amount of energy loss relative to pressure could be measured in Ki/(No/m2) = s3*m0.5/kg,
which really means (planar time)*(surface area)/sqrt(space of possibilities)/(mass-matter ratio) in this case, i.e. objects with a higher surface
area lose more energy from the same amount of pressure, objects with higher mass-matter ratios lose less energy from the same amount of pressure,
objects with higher spaces of possibilities lose less energy from the same amount of pressure, and of course the energy loss is multiplied by
the amount of planar time the pressure is applied for. This measurement can be used to measure how susceptible to having its energy changed by
pressure a particular material is, as the measurement of Ki*m2/No varies based on the materials involved.
 Chapter 3: Atoms and Molecules
Chapter 3: Atoms and Molecules
The next derived units to discuss are electrical units, but before we get to that, we need to understand how charges themselves
work in Lartraveran electricity, and since doing so involves understanding the equivalents of protons and electrons, we might as well discuss the
basics of Lartraveran chemistry on the atomic scale while we're at it.
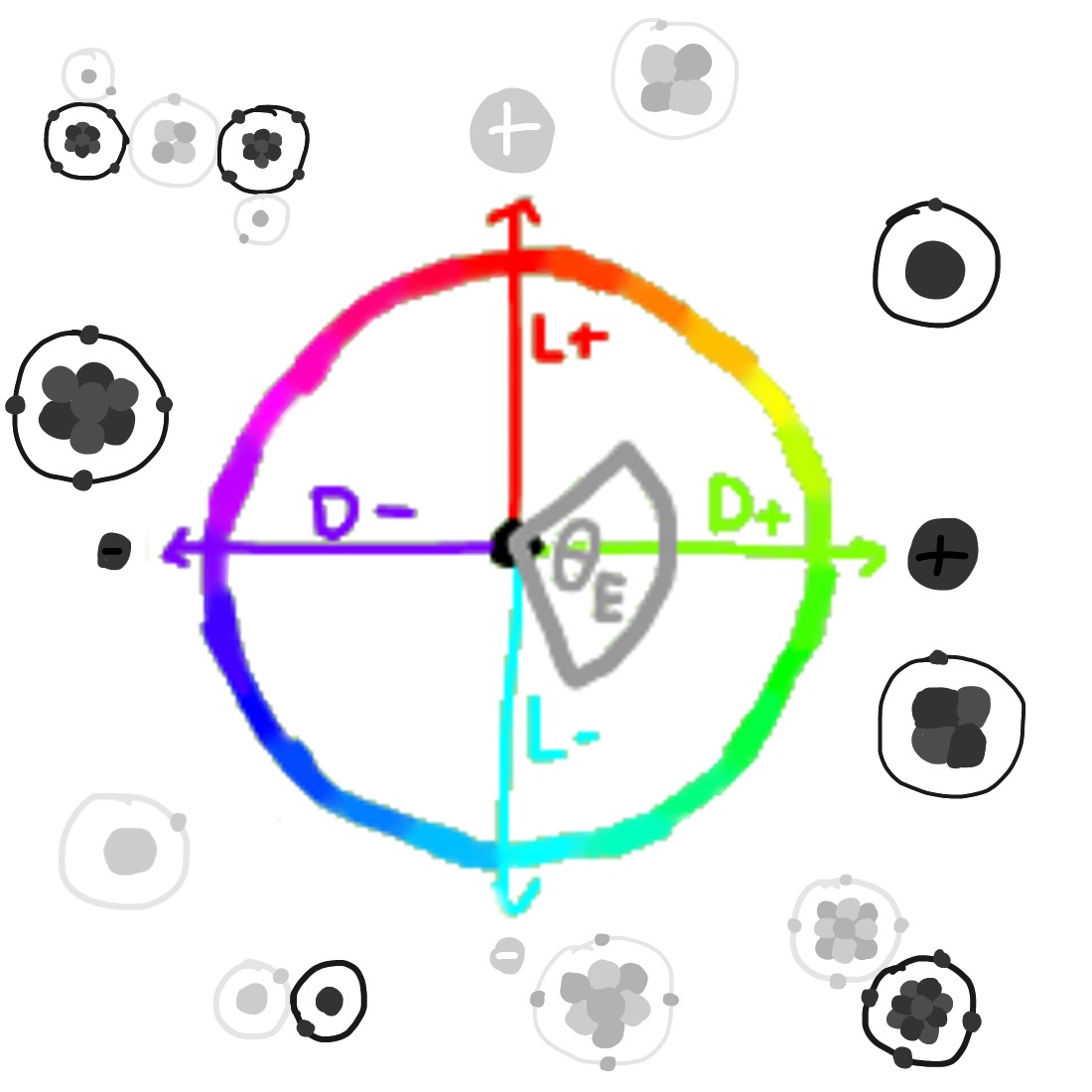
Two-Dimensional Electric Charge
Fundamentally, charges of single particles in Lartravera come in four varieties:
littra positive, littra negative, darra positive, and darra negative. In our world, the two types of charges are the only possible types of charge,
but since electricity is two-dimensional in Lartravera and charges of different matters will not cancel out, charge in Lartravera
on a macroscopic level comes in a full revolution of varieties. If we use a coordinate plane where
littra positive is north, darra positive is east, littra negative is south, and darra negative is west, then if you take 1 C of littra electrons
and 1 C of darra electrons, then by the laws of vector addition the system as a whole must have a charge of 1.41 C (sqrt(2), to be exact) southwest.
Of course, depending on the ratio of charged particles, electricity of practically any angle can exist on the macroscopic scale.
Since subatomic particles in Lartravera don't have mass (mass is an emergent property of objects thanks to the gressa phenomenon), forces that
affect subatomic particles such as electrostatic forces are matter forces,
which are very weak on the macroscopic scale but are strong on the subatomic scale
(the reason for this is simple: on the scale of individual atoms, a matter force's effect on a littra atom or darra atom is around the same as an
equivalent mass force's effect on a gressa atom, it's just that on the macroscopic scale there's orders of magnitude more gressa than there is
littra or darra, since the amount of mass of an object is on the scale of the square of its amount of matter). Like in our world, opposite charges
(charges at a 180° angle to each other, such as littra positive and littra negative) attract and alike forces
(charges at a 0° angle to each other, such as two darra negatives) repel. Perpendicular charges (charges at a 90° angle to each other,
such as littra negative and darra negative or littra positive and darra negative) do not exert any force on each other, while forces at a 45° angle
would repel each other but with a weaker strength than the repelling force of 0° forces. Since we're talking about angles, we can surmise that the
strength of the repelling force of two charges, relative to what the repelling force would be if those charges were of the same angle,
is multiplied by of the cosine of the angle, so in the 45° case the repelling force is around 0.707× the strength it would be for the 0° case
if the charges are identical in magnitude in both cases.
Atoms and Elements
So how do atoms work in Lartravera? Well, as I mentioned previously, atoms are exclusively made of one type of matter.
The reason for this is the strong nuclear force, which in Lartravera is only attractive towards nucleons of the same matter type as the nucleus
in question and is repulsive towards nucleons of the other matter type, hence atomic nuclei in Lartravera only consist of one type of matter.
Since atomic nuclei only consist of one type of matter, it follows that this also applies to atoms as a whole; a littra electron will be
electrically attracted towards a littra nucleus, but a darra electron experiences no electric force from a littra nucleus and thus will not
become part of its orbit. The atomic nucleus of an atom is what actually counts as an atom, and even a nucleus without any electrons will
still count as an atom in gressa creation; the quantum interactions that cause this originate from protons, but each proton in the same nucleus
doesn't count as an individual atom for gressa creation because the neutrons holding the nucleus together sort of absorb this effect and reflect it
cohesively so only the nucleus as a whole participates in the creation of gressa. However, atoms are NOT electrically neutral by default
in Lartravera. Instead of electron orbitals, atomic nuclei have fields that hold the atom together. While electrons are attracted by electric forces
and kept in orbit by these "proton fields", the proton fields also serve as a stabilizer for the atom, which among other things prevents additional
electrons beyond a certain amount from entering the atom as easily. These fields are more powerful when they're symmetrical, and their symmetry
comes in twofold layers, so they're at their strongest for atoms with an atomic number that's a power of 2, and still stronger than average
(but not quite as strong as for powers of 2) for an atomic number closely related to a power of 2 (such as 48, since that's three times 16).
This means that when you add an extra proton to a nucleus with a power of 2 of atoms,
the previously-completed field becomes weaker as it refactors to take on the symmetry of the next power of 2;
the field is stronger for each complete power of two than the last, but since this example leaves the field very incomplete,
the field becomes weaker and thus the atom accommodates several more electrons. Proton fields never strengthen enough with additional protons
to cause atoms with more protons to naturally hold less electrons than those with fewer protons, but often adding an additional
or even multiple protons to a nucleus may not change the amount of electrons it holds in a non-ionized state, where here "ionized" means its charge
is not the natural charge of that element. An element is still defined by its amount of protons in Lartravera,
and the periodic table looks like this:
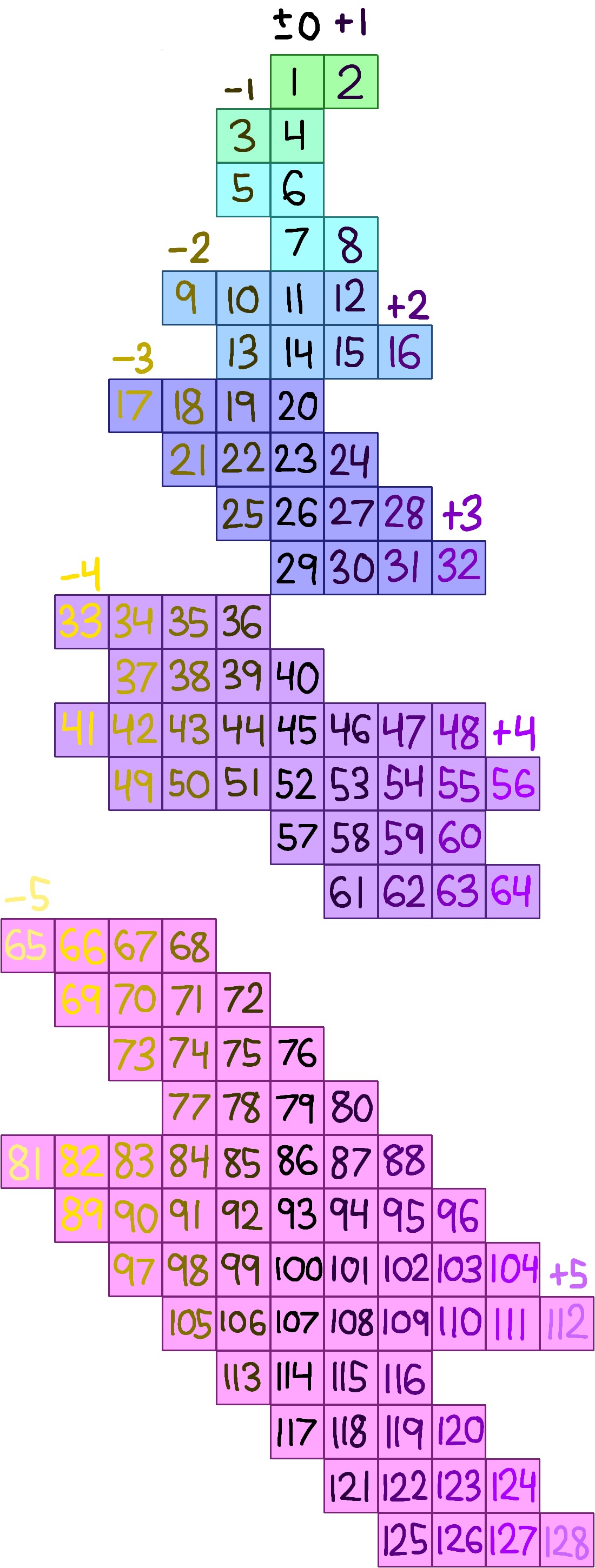
The number in each box is the atomic number of that element, while the column a box is in shows the natural charge of that
element. For example, element #35 is in the -2 column, so an atom with 35 protons naturally has 37 electrons. As you add protons to an atom
with weak proton fields, the proton fields become closer to symmetrical and thus stronger, until you reach a point of subsymmetry
(such as at element #12: the full symmetry being worked towards here is at 16, but the subsymmetries right now are 8 and 4, which at
this size of atom are fairly symmetrical themselves), at which point adding another proton causes the subsymmetry to be broken,
which causes the proton fields to become weaker, which causes the atom to naturally have more electrons. Elements with positive natural charges
tend to exist in lower-density states such as gases (the atomic nuclei repel each other with a stronger force than they're attracted to the
other atoms' electrons), while elements with negative natural charges tend to exist in higher-density states such as solids
(the atomic nuclei are attracted to the surplus of electrons with a stronger force than they repel each other).
This periodic table applies to both types of matter, as littra and darra obey the same rules, have the same types of particles, and thus have
the same elements. If you were given a scene in Lartraveran physics, you could tell that there are two types of matter,
but since littra and darra are symmetrical in the laws of physics, without a reference point it would be impossible to tell which type is
littra and which type is darra, and this is true for every law of physics,
like how it's true for matter and antimatter in our world.
Molecules
Whereas atoms are formed from one type of matter, molecules always contain atoms of both types of matter.
In order for a stable molecule to form, it must be electrically neutral, but the trick is that it's the square charges that must be equal:
the product of the littra protons and the darra protons must be equal to the product of the littra electrons and the darra electrons to
form a stable molecule. Once a stable molecule has formed, the electrons become less tied to individual atoms and more tied to the molecule as a
whole, which means that two-matter charge becomes important for intermolecular interactions. Whereas particle (linear) charge can come in any angle,
molecular (square) charge only comes in four signs, which correspond to northeast (both positive), northwest (littra positive, darra negative),
southeast (littra negative, darra positive), and southwest (both negative) respectively: since the two particle charges are being multiplied
rather than added, only their magnitudes matter when determining the magnitude of the molecular charge, and only their 1D signs matter when
determining the sign of the molecular charge. Furthermore, because of the way molecule formation works, northeast and southwest are the only
possible directions of molecular charge in most cases (since littra positive and darra positive multiply to make northeast while littra negative
and darra negative multiply to make southwest). Some notable consequences of the way molecules work in Lartravera is that electrically neutral
elements naturally exist in a diatomic state where each molecule contains one littra atom of that element and one darra atom of that element:
for example, a molecule containing one littra atom of element #4 and one darra atom of element #4 contains four littra protons
and four darra protons = 16 e2 NE, and four littra electrons and four darra electrons = 16 e2 SW, and since the
opposing charges cancel out, the molecule is electrically neutral and is thus a stable molecule, and if a molecule contains at least one
electrically positive atom of one type of matter then it must also contain at least one electrically negative atom of the other type of matter,
and vice versa. There are obviously symmetric molecules that contain the same littra atoms as darra atoms
(the simplest of which is obviously a diatomic molecule containing one atom of element #1 of each matter type), but there are also asymmetric
molecules where the atoms of the two matter types are different but the molecule still turns out electrically neutral. The simplest of these,
which in this case means "smallest amount of squared charge to cancel out", contains one atom of element #4 of littra and four atoms of element #1
of darra or vice versa: in this arrangement, there are four littra protons and four darra protons = 16 e2 NE, while there are four
littra electrons and four darra electrons = 16 e2 SW, and since those charges are the same magnitude and opposite "direction",
the molecule is electrically neutral and stable. It's also possible for an asymmetric molecule to have a neutral molecular charge but a
nonneutral particle charge: the simplest molecule of this kind contains one atom of #2 and two atoms of #1 of littra, and two atoms of #3 of darra,
or vice versa: in this arrangement, there are four littra protons and six darra protons = 24 e2 NE, while there are three littra electrons
and eight darra electrons = 24 e2 SW; this molecule has no net molecular charge and is thus stable,
but its particle charge is not neutral, as it has a +1 littra particle charge and a -2 darra particle charge.
 Chapter 4: Electrical Units
Chapter 4: Electrical Units
There is perhaps nowhere where more named derived SI units are used, even in countries where the metric system isn't used
(i.e. the United States), than in electricity. We saw in Chapter 2 that some of the mechanical units are different than in Lartravera than in our world,
and that's true of electrical units as well. In this chapter, I'll go over electrical units, but first I have to discuss some other electrical concepts
that lead into the units.
Ezzolmisation
The electrostatic force in Lartravera actually comes in two forms. We've already established the matter force,
which would have an electrostatic constant defined in the dimensions of No/kg*m2/C2 since it's based on the particle (1D)
charges of the two particles in question, but there's also a variant of the electrostatic force that scales at the rate of a mass force
and is thus powerful on the macroscopic scale. This electrostatic force occurs between molecular charges and is thus based on the 2D charges of the
two particles in question, so that electrostatic constant would probably be defined in the dimensions of No*m2/C4.
But how do you cause this force? You can't use currents of electrons because they have no mass or molecular charge, and molecular charges are,
well, on a molecule-by-molecule basis rather than for the object itself like mass is, and since all molecules are electrically neutral,
any object made of stable molecules must also be electrically neutral. Individual electrically charged atoms can't be used for this either,
as they won't link together to create molecular charge unless doing so would result in an electrically neutral molecule. The key to giving an object
a non-zero molecular charge is in linking molecules together in a process called ezzolmisation. In an ezzolmisated object, the molecules are
electrically linked together, meaning that rather than subtracting the products of the charges in each molecule, you take the product of the
positive charges in the object and the product of the negative charges in the object and then subtract those to get the total molecular charge
of the object, as if the whole object is one giant molecule.
Ezzolmisation serves no electric purpose in an object that's made of only one type of molecule, but in an object that's made of multiple molecules
that have different ratios of protons and electrons, ezzolmisation can in fact result in giving an object a non-zero molecular charge:
for example, if we look at a tiny object containing 10 L2L12D32 molecules
(the smallest particle-charge-nonneutral molecule from earlier) and 10 L1D1 (diatomic element #1) molecules,
then the object will contain 50 littra protons, 70 darra protons, 40 littra electrons, and 90 darra electrons.
In a standard molecular state, these particles are partitioned into those molecules that result in the square charges canceling out,
but in an ezzolmisated state, those full numbers are the ones multiplied: the protons result in 3,500 e2 NE,
the electrons result in 3,600 e2 SW. These charges will not cancel out completely, as 100 e2 SW will be left over,
so the object will have a molecular charge of 100 e2 SW. Ezzolmisation doesn't have to happen to a whole object,
as the ways it can be induced can also apply to portions of objects. This allows for piecewise ezzolmisation, where an object has thousands
or more of tiny portions of it ezzolmisated. Piecewise ezzolmisation generally results in less total molecular charge than if the entire object
is ezzolmisated, but it allows these portions of the object to exert electrostatic molecular force on each other, and this is how currents using
molecular charges and mass force work. Electric circuits using the particle charges of currents of electrons do exist, and since particle electricity
has a full 360° of charge values there's all sorts of designs for such circuits, but more advanced civilizations tend to use molecular charge
currents with the moving particles being clumps of molecules in the object that have been piecewise ezzolmisated, as mass forces are much stronger
than matter forces and thus allow for a much greater transfer of energy.
An Example of an Energy Source
It's good to keep in mind that electricity is not usually a power source itself; like in our world, the usual use of electricity
is to transfer energy rather generate it (in Lartravera's case, this is because electrostatic forces are matter forces and are thus very weak on the
macroscopic scale). In our world, we have sources of power like chemical reactions (burning fossil fuels, for example), nuclear reactions
(nuclear power, duh), spinning a turbine to generate kinetic energy (hydro and wind), using the energy from photons (solar), and so on.
Lartraveran societies also often have several sources of energy, but there's a notably efficient one that specifically relies on the way energy
works in Lartravera. Since energy increases with volume of possibilities, if we place a fast-moving particle or clump of particles in a large
chamber, then we close in the walls, we're reducing the volume of possibilities and thus the energy of the particle.
We can then use electric currents to absorb some of that lost energy and transfer it. Once the chamber has gotten small enough that there isn't
much more energy to extract, the chamber is re-expanded, the now low-energy particles are transferred to a larger inactive chamber to allow their
energy to naturally increase again while another clump of particles goes in the chamber, and then after enough clumps the cycle repeats.
Like all sources of energy, this is finite in theory, but since the particles can absorb energy from things like the air while in waiting,
compression power is an energy source that often lasts a very long time before the surroundings grow low on energy and the power building is either
abandoned for a new location or converted into another form of power... and since all processes are reversible in Lartravera thanks to the nature of
time, the lifespan of power sources is extended even further than it would be if they couldn't be reversed, as energy can always be pumped back
into the power source to get it going again.
Now that we can understand the fundamental ideas of both particle charge and molecular charge,
we can finally discuss electric units.
Charge Ratio and Voltage
The ampere is still coulombs/second and is thus particle charge per linear time,
while squared amperes are C2/s2 and are thus molecular charge per planar time; A2*s = C2/s is the unit of
molecular charge per linear time. C2/C is the unit of charge ratio, the ratio between molecular charge and particle charge,
which is useful in circuits that contain both particle charge sections and molecular charge sections. However, I feel that charge ratio is
significantly less useful than mass-matter ratio, and the more useful unit is C2/kg2, the amount of molecular charge per mass
in an ezzolmisated object or piece of an object; since doubling littra and darra in an ezzolmisated object quadruples both mass and molecular charge,
this unit is independent of the mass of the object and can thus be used to measure "ezzolmisatability" of a particular combination and ratio
of molecules.
Voltage for a particle charge circuit can be measured in Ki/C, but what about a molecular charge circuit?
Well, if we double the littra and darra of each ezzolmisated piece and examine a pair of pieces, we've quadrupled the molecular charges of both
objects, which multiplies the total electrostatic mass force by 16, but energy/force is inversely proportional to mass-matter ratio and doing this
doubles the mass-matter ratio. Still, doubling the matter amount multiplies the energy from the electrostatic mass force by 8, which is more than
the 4× that was expected. As such, while voltage as "the amount of energy gained from a circuit per molecular charge" could still be measured as
Ki/C2 (a unit which I'm calling the Wezitep (Wp)), that value changes depending on the sizes of the pieces used, so if we want the more
common (in our world) use of voltage as a constant property of the circuit, then Wp/C2*(kg2/kg) = Ki/C4*kg is
probably the unit you're looking for.
Storing Electrical Energy
Capacitors store electrons between their plates in order to store charge, so since the energy gained from molecular charge
increases with larger ezzolmisated pieces, using capacitors to store molecular charge doesn't really make much sense because eventually you'd just
have chunks of solid material lodged in the plates. The unit of capacitance can be defined as C/(particle voltage) = C/(Ki/C) = C2/Ki
much like in our world (this may look like the inverse of the Wezitep, but that C2 isn't molecular charge) for a particle circuit,
but for molecular circuits capacitors aren't used to store electric energy. Instead, ezzolmisation itself is used to store electric energy for
molecular charge. Since ezzolmisation involves linking molecules together in a way that they'd prefer to not be linked, it's a higher-energy state
than the naturally electrically neutral state of individual molecules. This means that one way to build a circuit for a device that has to be able
to store charge is to place an object inside a circuit (whether particle or molecular), use the energy in the circuit to ezzolmisate part of the
object, then when the charge is needed, have the mechanisms of the circuit slowly disezzolmisate the object by disezzolmisating sections of it
continuously, which allows the release of the energy contained within the ezzolmisation. Under this method, 100% charge means the
"ezzol storage object" is completely ezzolmisated, while 0% charge means that the object is in a molecular-electrically neutral state.
Ki/C2 thus becomes a useful unit to describe the energy gained from this disezzolmisation, which is why I chose to name it the Wezitep
rather than saving that name for the constant voltage unit of Ki/C2*kg. There is a catch to this, however. Ezzolmisation isn't a
completely stable state, as the more non-ezzolmisated (or even ezzolmisated but on a smaller scale) molecules hit and interact with an ezzolmisated
cluster of molecules, the more likely it is that some of the molecules will break away from the ezzolmisation and either form a smaller ezzolmisated
cluster or just return to a non-ezzolmisated state. This means that an object that's completely ezzolmisated and is floating in empty space is
very likely to stay ezzolmisated, while the ezzolmisation of a cluster of molecules in an object which is non-ezzolmisated throughout the rest of it
is much more likely to have its ezzolmisation decay quickly. Because of this property of ezzolmisation, an ezzol storage object with 100% charge
will keep its charge for much longer than an object with a lower percentage of its maximum charge, though the fact that molecular charge decreases
at a lower rate when there's less of it (because it works off the product of littra charge and darra charge) helps combat this.
Still, tracking charge percentage on a device using ezzol storage in a way that makes it look linear to consumers is a tricky task for
Lartraveran electrical engineers!
"Resistance" in Molecular Charge Circuits
Resistance means something very different for molecular charge circuits than it does for particle charge circuits,
and that's because of the different structure between the two. In a particle charge circuit, electrons are traveling through a conductive
but solid material, which makes resistance dependent on the material and its shape. In a molecular charge circuit, the charge flowing through
the circuit is clumps of ezzolmisated molecules, and since the point of these circuits is to let electrostatic mass force act and mass force in
Lartravera causes expansion in space of possibilities, it makes more sense to make molecular circuits hollow and wide, and since they're moving
through the empty space inside the circuit rather than through a material, resistance doesn't really apply. There are, of course, situations in which
we do want resistance to apply in order to transfer energy (such as turning electric energy into heat energy), and in this case physics is in our
favor, as force itself can have an element of resistance to it. Forces change the rate at which space of possibilities expands over planar time,
so when a positive (repulsive) force applies for long enough and strong enough that some of the space of possibility expansion it would have caused
on its target in empty space is canceled out by other objects blocking some of the space, then you get a resistance to the force itself,
which is like another object pushing back against the moving object in our world, except in Lartravera the object doesn't have to be actually
pushing against the barrier at the point in time in question, it just has to be pushing against the barrier somewhere within its volume of
possibilities within the area of time that the force is being applied for. In most cases, this means that there will always be some resistance
to all forces. Since this resistance is changing the rate at which space of possibility changes, we can measure it in
((m3/s2)/s2)/No. This technically reduces to 1/kg2, showing that the amount of space of possibility
change (usually reduction) caused by this "possibility pushback" is inversely proportional to the object's mass assuming a constant force...
but this makes sense, since a given force's effect on space of possibilities is less for more massive objects, so there's less of an effect to
reduce. Possibility pushback can be measured in kg-2 when examining the space itself and how any object experiencing a repulsive force
at a point within that space will have the force's effect reduced by it, but it often makes more sense to factor out the mass and just treat
possibility pushback as a dimensionless ratio or percentage of the force's effect on space of possibilities that isn't going through.
Of course, depending on the shape of the space, the possibility pushback ratio can easily increase and decrease the longer the force is applied for.
It's also good to keep in mind that it's not always the case that 100% of the positions that would hit the barrier are pushed back and not added to
the volume of possibilities. In the case of two similar-sized objects, some of the force that doesn't go through to the original object is obviously
being used to push the blocking object instead. In the case of a tiny molecule clump pushing on the walls of the circuit, with enough force the
clump may push its way partway into the wall in some of the points in time the force is being applied to, so some of the points in the wall will
still be in the clump's volume of possibilities. Even if possibility pushback is a factor, energy/force is still roughly the same,
(in fact, since average space of possibilities is reduced, energy/force is actually increased a bit), which means if not all
of the force is expanding the space of possibilities, some of the energy must be going into the barrier material,
which depending on what we make the circuit out of may be able to be transferred from there. This means that we can take advantage of
possibility pushback at specific points by changing the width and shape of the circuit... okay, this is getting too specific, isn't it?
The point I'm trying to make here is that since molecular charge circuits are usually hollow and use solid moving pieces, typical electric resistance
(which is how hard it is for charge to move through a material) doesn't apply, but we can use resistance to space of possibility expansion
at the walls of the circuit instead. Even if the circuit is made out of solid material, electrical resistance still doesn't really apply for
molecular charge, as the solid material blocking the molecule clumps from physically moving does far more than the resistance caused by the
charge.
Magnetism
In our world, magnetism is a force caused by moving charges, and that's still true in Lartravera.
However, its effects and results are quite different than in our universe. In our universe, magnetic fields have all sorts of strange rules
with their effects on moving charges based on perpendiculars and angles, but in Lartravera it's arguably simpler.
The magnetic fields generated by moving charges are in the same direction as their velocity, and they cause some particles to be attracted in
that direction and others to be repelled. Unlike electrostatic force, this does not follow the rule of
"opposite charges attract, like charges repel"; instead, charges at a 0° angle and charges at a 180° angle both result in the magnetic field
exerting repulsion, and it's charges at 90° and 270° angles that cause magnetic attraction. If we consider that repulsive forces are positive
and attractive forces are negative by definition, then while the electrostatic force has a multiplier of cos(θ), where θ is the angle between the
charges, magnetic field force has a multiplier of cos(2θ). On the level of individual charged particles, Lartraveran magnetism results in
"opposite matters attract, like matters repel", which means that magnetic forces are a big part of why littra and darra are never seen
apart from each other on the macroscopic scale. This still only applies to moving particles, though, which means that magnetism doesn't do much
harm to the strong force's repulsion of opposite matter at a subatomic scale. The Lartraveran equivalent to the tesla would be
"The magnetic field strength that causes a 1 C particle charge to be repelled with a strength of 1 No when moving at 1 m/s, given that the
magnetic field's electric angle to the particle charge is 0° or 180°", and so much like in our world we can measure in No/(C*m/s) = No/(A*m),
which in base units (Let's be honest, the coulomb is much more of a base unit than the ampere, especially in Lartraveran physics)
is kg2*m2/s3/C. Because magnetism acts as an attractive force between charged littra and darra,
it's the property responsible for the formation of molecules. Charged littra and darra particles in atoms attract each other
to start the process, then electrostatic force helps attract opposite charges to the building charge to work towards electric neutrality.
However, magnetism is a matter force, and while molecules do have individual masses (but the whole is greater than the sum of its parts
when it comes to mass) individual atoms do not, so electrostatic forces acting during molecule formation are also typically matter forces.
There is, however, a third force involved, a force that only manifests as a combination of electrostatic and magnetic forces,
a force which I'm going to call molecular magnetism. Molecular magnetism has the strength of a mass force since it deals with molecular charge,
but it sort of acts on matter rather than mass, and here's a simplified explanation of how it works: when an atom gets close enough to an
unfinished molecule, molecular magnetism acts as if that atom is already part of the molecule. If that atom's addition causes an increase
in the squared charge of the unfinished molecule, then molecular magnetism effectively causes the atom to be repelled. If that atom's addition
causes a decrease in the squared charge of the unfinished molecule, then molecular magnetism effectively causes the atom to be attracted.
Molecular magnetism's name is somewhat misleading, as it cares only about the squared charges and not the velocities. However, molecular magnetism
is exerted on the passing atom by all of the matter in the molecule, so a larger molecule exerts stronger molecular magnetism.
Therefore, the universal constant of molecular magnetism would be measured in No/kg/C2, where C2 refers to the amount of
squared charge the passing atom would add to the molecule. Since molecular magnetism doesn't grow stronger for moving molecules,
if we align the magnetic fields in an object or part of an object correctly and get the molecules moving fast enough,
we can make particle magnetism stronger than molecular magnetism for that part of the object, and this results in ezzolmisation.
Alright, I think I've covered enough for this part. I don't exactly have a perfect understanding of how electricity, currents,
magnetism, etc. work in our world, so I may have gotten some things wrong about how they work in Lartravera.
If there's anything you think I missed, please let me know at mathcookie17@gmail.com.
 Chapter 5: Streggis and Temperature
Chapter 5: Streggis and Temperature
The other base units I've discussed so far would have similar meanings in Lartravera as they do in our world. Distance, time,
mass, electric current, amount of atoms... though the way they each work is (except for distance) different than in Lartravera than in our world,
the basic concept is generally the same... but not for temperature. Though Lartraveran "temperature" has similar macroscopic effects to temperature
in our world, the microscopic details, and indeed the very definition of Lartraveran temperature, is quite different than in our world. In fact,
the Kelvin wouldn't even be a base unit...
What is an Object?
In our world, there's no such thing as "objects" in the fundamental laws of physics, as objects are a macroscopic phenomenon
caused by atoms and molecules bonding together. However, as you've probably gathered, Lartraveran physics DOES have a formal definition of what an
object is: an object is a closed system for the gressa phenomenon, which means that a single littra atom will make a gressa atom with
every darra atom in that object and vice-versa, but the gressa phenomenon cannot travel between objects. In other words, an object is
defined as a clump of matter in which the gressa phenomenon can freely spread within the clump but not travel outside it. In many cases, this
definition of an object coincides with the macroscopic usage of the term that we're used to, but sometimes it doesn't. For example, certain types
of glass in Lartravera are made of a bunch of microscopic clumps of matter that are separated just far enough that the gressa phenomenon
can't permeate between them, resulting in an extremely light material on account of its incredibly low mass-matter ratio. A pane of this glass
may feel like a single object macroscopically, but by the Lartraveran physics definition of an object it's actually many, many tiny objects,
not one large one.
Gress-Waves, Proton Fields, and Streggis
If the gressa phenomenon is what defines an object, then how does the gressa phenomenon work? We know that in a single instance
of the gressa phenomenon, each littra atom interacts with every single darra atom and vice-versa, and each interaction creates a single gressa
"atom". Gressa atoms can have different masses: the more matter the two matter atoms that created a given gressa atom have, the more mass the gressa
atom has. We also know that it's caused by atomic nuclei: it originates in protons, then the neutrons absorb and reamplify it so that the single
nucleus as a whole only sends a single piece of the interaction. It's believed that the gressa interaction propagates through matter:
a single "wave" of this interaction, which I'll call a gress-wave, originates from one atomic nucleus and can travel between atomic nuclei.
Though a gress-wave will only contribute to a gressa atom's creation (and only halfway: gress-waves come from both types of matter, and forming a
gressa atom requires a littra atom's gress-wave to hit a darra atom and for that darra atom's gress-wave to hit that littra atom in return,
though if a gress-wave can travel from one atom to another then a gress-wave can definitely travel the other way around as well, so this is a moot
point) when it passes through a nucleus of the opposite matter as the gress-wave, gress-waves can still travel through matter of the same type,
so even a hypothetical object with all the littra in one half and all the darra in one half could still be a single object. Gress-waves can only
travel a certain distance without jumping to another piece of matter, and this distance is usually on the scale of picometers and nanometers.
This distance is dependent on several factors, and the first is energy: the more internal energy an atom has, the farther gress-waves from it are
able to travel.
The second factor that this is dependent on is the proton fields of the atom. Gress-waves are transmitted via proton fields, and so
atomic nuclei with stronger (i.e. more symmetric) proton fields also allow gress-waves to travel farther. Proton field strength from symmetry can't
really be measured using an existing unit, as while it does cause electric force, it's more of its own quantity and electric force is just one of
the things it does. The electric forces and the gress-wave traveling distance are both related to proton field strength, but their relation to each
other is mostly nonexistent, as proton field strength in an electric force context means something very different than it does in a gress-wave context.
To define the latter, we'll need a new base unit, which measures a quantity I'm calling "streggis". Streggis is the word in my Lartraveran translation
system for "proton field strength in the context of the gressa interaction", and it's a word that falls in the same category as the words
"distance", "time", "mass", and "temperature". Doubling the internal energy of an atom doubles its streggis, and atomic nuclei with
higher-symmetry proton fields have a higher streggis. I'm calling the metric unit of streggis the "salligregi" (sg), and to define it, we can use the
fact that dividing streggis by energy gets you a unit that purely measures proton field symmetry, a unit that has a single value for each element.
As such, one possible definition for the salligregi is by defining, say, the proton field symmetry of some chosen element as some chosen value of
sg/Ki. This means that the proton field symmetry value of that element is the universal constant used to define the salligregi, like how the meter is
defined by the speed of light, the kilogram is defined by Planck's constant, and the second is defined by "the period of transition between hyperfine
levels of a ground-state atom of caesium-133", whatever "hyperfine levels" means... of course, those are the definitions of those units in our world,
and other civilizations, even in our universe, would have different definitions for units of the same dimensions; the definitions in Lartravera would
be even more different. If multiple civilizations use that "proton field symmetry of an element" definition for the unit of streggis, then they'd
probably choose different elements and different values that best suit the way they do science; lifeforms on planets with different abundant
elements and different sizes of life are likely to have different exact definitions even under this general principle. The exact value of the
salligregi doesn't matter for our purposes, what matters is that it's a base unit, it measures streggis (a.k.a. proton field strength in the context
of gress-waves), and it's defined by defining sg/Ki as a unit of proton field symmetry because streggis increases with internal energy.
Gressange
The streggis of an atomic nucleus isn't enough to determine how far gress-waves can travel, as other factors
(such as velocity/kinetic energy of moving particles, the ratio of the two matter types
(but not mass-matter ratio since it's gress-waves that create mass in the first place), or the ever-important space of possibilities)
can play a role as well. To determine how far gress-waves can travel, we can use a quantity called "gressange", which as the name implies is
sort of a "range of gress-waves"... but it's not measured in plain distance units. Gress-waves don't really travel through the space between atoms,
and in fact "gress-waves" are probably just a simplification rather than an actual wave. Because of this, it makes more sense to say that a
gress-wave instantly jumps between atoms rather than travelling from one to the other. When a gress-wave is traveling between two atoms,
whether it can make the jump is based on the product of the gressange of the atom it's at and the gressange of the atom it's jumping to.
Since multiplying these gressange values gets you the distance (which can be measured in meters, though normally a smaller unit would be used)
the gress-wave can travel in the interaction between those two atoms, it makes sense to measure gressange in a "square root distance" unit,
such as m0.5. Gressange is a property of the atoms, not the gress-wave itself; whether the gress-wave can make the jump between two atoms
has nothing to do with the atom the gress-wave originated from, only the atoms it's jumping between.
Temperature at a Microscopic Level
So how are streggis and gressange related? This is where temperature comes in: the higher the temperature of atoms of the same
streggis, the higher their gressange. In fact, this is how temperature is defined in the model of Lartraveran physics I'm using.
The unit of temperature (which I'm still calling the Kelvin for the sake of understanding, even if the definition is different) is not a base unit
in this model of Lartraveran physics; instead, 1 K is defined as 1 m0.5/sg, i.e. the temperature at which atoms with 1 sg will have a
gressange of 1 m0.5. Whereas gressange is a property of atoms and not gress-waves, it kind of makes sense to consider temperature
as a property of gress-waves, with temperature only applying to atoms as a measure of the temperature of the gress-waves they create.
I mentioned in the first part of this analysis of Lartravera that the temperatures of the two types of matter in a single object are independent
values, and that's because of how gress-waves interact with atoms of the same matter as their origin. When a gress-wave originating from one type
of matter jumps to an atom of that same type of matter, the gress-wave's temperature and the atom's temperature become a bit closer to each other,
like how objects in our world have their temperatures become closer to each other when in contact. Since gress-waves act on atomic (i.e. very small)
time scales, the atoms of one type of matter in an object influence each other very quickly, causing all the littra atoms in an object to quickly
reach a single equilibrium temperature and all the darra atoms in an object to quickly reach a single (but often different) equilibrium temperature,
but these two temperatures don't influence each other because the gressa waves interacting with the opposite matter are creating gressa rather than
influencing temperature.
Temperature at a Macroscopic Level
Squared temperature refers to the product of the littra temperature of an object and the darra temperature of an object,
and since the distance gress-waves can travel is based on the product of the two temperatures, it's squared temperature that exhibits most of
the macroscopic properties of temperature. Since 1 K = 1 m0.5/sg, 1 sg = 1 m0.5/K, and therefore
1 sg2 = 1 m/K2, meaning that squared salligregi can be used to measure the average distance gress-waves can travel
assuming a given squared temperature.
Temperature may not be defined by average kinetic energy in my model of Lartraveran physics, but squared temperature
(which I will call macroscopic temperature or "macro-temperature" starting now) still exhibits many of the same properties as temperature in our
world. Since streggis increases with energy, and temperature has streggis in the denominator, you may think that higher temperatures in Lartravera
result in less energy, but that's not true. Since increasing temperature allows gress-waves to travel farther, the atoms in the object tend to
spread out further. This means they can attain a higher space of possibilities, which in turn gives them more energy... and this increases streggis,
so the cycle repeats. The cycle eventually peters out due to conservation of energy, but because of this temporary feedback loop,
heating an object in Lartravera by only a little bit can result in a much larger increase in temperature than you may expect.
Objects in contact slowly cooling/heating each other until they reach an equilibrium temperature is a fact of temperature in our world,
and this holds in Lartravera too. When two objects are in contact, the randomly-vibrating/moving atoms within the objects occasionally get close
enough that a gress-wave can jump from an atom in one object to an atom in the other object. Any gressa atoms created by these gress-waves will
vanish near-instantly since the gress-wave interaction isn't sustained, but the temperature reaction will happen and persist. Since these gress-wave
crossings happen far less often than gress-waves permeating through a single object, the two objects influence each other's temperatures on
macroscopic timescales rather than the atomic timescales that temperatures in a single object equalize each other, but given enough time,
the temperatures of two objects in contact will approach an equilibrium: their littra temperature will approach a value between their original
littra temperatures, and their darra temperature will approach a value between their original darra temperatures, therefore their macro-temperature
will approach a single value as well.
States of Matter
As you continue to heat an object and the cycle of energy increase plays out, eventually the object will reach a critical
macro-temperature, where the streggis is enough that the atoms are able to spread apart much farther than before and the cycle goes much higher
than at any other point. As you cool down an object, the cycle plays in reverse (atoms end up closer together, so less space of possibilities,
so less energy, so less streggis, and repeat until it simmers down), and there's a critical point there too. These critical points are where state
of matter changes occur, as the change in state of matter is caused by the critical-strength heating cycle or cooling cycle and is what
makes the critical-strength cycle so strong. Unlike in our world, an object's melting point and its freezing point are different:
when a heating object hits its melting point and enters the critical-strength heating cycle, the cycle ends at its freezing point,
and if it goes below the freezing point then the critical-strength cooling cycle kicks in and returns it to its melting point.
The macro-temperatures in-between the two are "forbidden temperatures", temperatures which that object cannot remain in because it will only
attain that temperature in the middle of a critical-strength heating or cooling cycle. These rules for melting and freezing points also apply to
boiling and condensing points. The states of matter in Lartravera include the typical solid (constant shape, volume, and mass) and liquid
(variable shape, constant volume and mass), but there are two types of gases. The type I'm going to refer to as "gas" has a variable shape and
volume, but the atoms still remain close enough for gress-waves to travel through them (because at that high a temperature gress-waves can travel
pretty far... well, pretty far for the atomic scale, anyways) so gases are still objects, and as such they have a maximum volume. However, if you
heat a gas to an even higher temperature, it can reach a point where the atoms drift too far apart for gress-waves to reach. Beyond this point,
the matter is in the "permeate" state, in which it no longer constitutes an object and no longer has mass (aside from the tiny masses of individual
molecules), it's just a bunch of atoms and molecules floating separately from each other. Since the gas -> permeate transition is the point at which
gressange stops holding atoms together, there's no heat cycle above that point, and so the permeation point of an object is both the point of the
gas -> permeate transition and the point of the permeate -> gas transition. Plasma isn't really its own thing in Lartravera: atoms are already not
always particle-electrically neutral so the definition of "ionized gas" isn't necessarily different from normal gas or permeate, and as for non-zero
molecular charge matter, that can be induced with ezzolmisation in most states of matter, so ezzolmisated gases aren't considered a separate state
of matter, and permeate molecules are too far apart to be ezzolmisated.
Solid, liquid, gas, and permeate are the main four states of matter in Lartravera, but there are some non-standard states as well.
As an object's temperatures approach zero, substances can reach a point where the gress-waves just can't travel far enough to reach other atoms
and the atoms can't get any closer thanks to their electrons repelling each other. This is called nodolib state, and matter in nodolib state is
solid in the sense that it maintains a constant shape and volume, but there's no gressa and thus no mass. There's a very small selection of
molecules that, when ezzolmisated, become held together so tightly that they'll retain their shape even as a gas. This is known as the "dialati gas"
state, and the volume of a dialati gas can be changed, but the dialati gas will keep its same shape and expand or contract uniformly when it
expands or contracts. Rumors have it that some advanced civilizations have found cosmic matter in a dialati permeate state, but given that matter
in the permeate state doesn't stay together and molecules in permeate state can't be ezzolmisated (because they're too far apart to be linked),
these claims are heavily disputed. Finally, some advanced civilizations have found use for an artificial kind of matter which I'm calling
"bariless goop", in which the atoms are kept at liquid temperature and surrounded by quantum barriers that prevent gress-waves from travelling,
resulting in a massless liquid-like state like how nodolib is a massless solid-like state and permeate is a massless gas-like state.
There are other exotic states of matter too, but since I've now covered all eight possibilities of retaining/not retaining constant shape, volume,
and mass, I think I've said enough about the states of matter, especially since only four or five of them really occur naturally.
Electron Fields
Atomic nuclei have proton fields that hold atoms together, repel electrons, and facilitate both temperature and the
gressa interaction, but what about electrons? Do electron fields exist? They do, but they're not as multifaceted as proton fields are.
Electron fields are weaker than proton fields since electrons contribute less matter than protons (this is Lartravera's equivalent of electrons
in our world having less mass than protons, but in Lartravera neither of them has mass on their own because matter and mass are distinct
concepts, so it's the matter amount that's different), and this weakness is furthered by the fact that electron fields are more spread-out
than proton fields (which are concentrated in the nucleus thanks to the neutrons). However, electron fields are still very important for one
reason: they facilitate the formation of molecules. The electron fields of a single atom will almost always be merged into a single collective
electron field. Electron fields have a charge, that being the collective charge of the electrons in the field. Electron fields can merge no matter
their charge. Electron fields do not have a significant effect if they only have particle charge since that charge comes directly from the
electrons within it... and from the protons. Since the electron field covers the whole atom, the charges of the protons are also factored into it,
so an atom with 47 littra protons and 45 littra electrons would have a collective electron field charge of 2 e north. When two atoms become
close enough to form a molecular bond, their electron fields merge. This is actually the definition of a molecular bond in Lartravera:
two atoms are molecularly bonded if they're within the same electron field, and for this reason, collective electron fields are often called
molecular fields. These molecular fields are where molecular charges come into being: all the electrons in the field zipping around and passing
by each other pool their charges together, as do all the protons in the nuclei in the field, and that's why molecular charges in a molecule are
gained by multiplying the positive charges and multiplying the negative charges first and then subtracting them (rather than subtracting for each
of the two matters first and then multiplying, which is what happens in non-molecular matter). If a molecular field has a non-zero molecular charge,
it becomes unstable, as the field starts repelling itself apart. When a neutral molecule is approached by a spare atom, that atom's electrons merge
into the molecular field, and this gives the molecule a non-zero molecular charge, then the field will become self-repelling, pushing everything
in the molecule apart. Since the approaching atom is at the edge of the electron field, it will most likely be pushed out of the field before
the rest of the atoms in the molecule can be pushed much, and so the molecule will return to its neutral state. However, if the approaching atom
decreases the repulsion (by decreasing the molecular charge of an unstable molecule), it's more likely to get close enough to the rest of the
atoms of the molecule that electric attraction and/or magnetic attraction can outweigh molecular repulsion.
These two cases are the force I previously referred to as "molecular magnetism", and since the electrons facilitate this force,
molecular fields are stronger the more electrons they contain. This means that two or three atoms can bond
even without being molecularly neutral because the molecular field between them is weak and forces like regular magnetism will
hold the atoms together, but the more atoms a molecule contains, the harder it is for new atoms to join, especially if
said atoms give the molecule more molecular charge rather than reducing it. The fact that atoms have to briefly join a molecule in order to be
repelled by it means that objects that appear to have a neutral molecular charge technically always have tiny amounts of molecular charge that
are appearing and disappearing on atomic timescales, but this can generally be ignored on the macroscopic scale. If the radius of a proton field
is the radius of the atom, then the radius of the molecular field is the radius of the molecule, since anything inside the molecular field is
part of the molecule while anything outside the molecular field is not part of the molecule. While the radius of an electron field becomes larger
based on many of the same factors as those that increase gressange (velocity, space of possibilities, etc.), electron fields don't specifically
rely on both matters to exist (but they do rely on both matters for the molecular bonding: if two atoms of the same matter pass by each other,
their electron fields may merge for a moment, but there's no magnetism holding them together so they'll probably split again), so the effect of
the number of electrons on the radius of the field is linear rather than quadratic. Since electron fields are weaker than proton fields,
the radius of a molecular field is almost always smaller than the distance that gress-waves from the atoms in the field can travel. If this wasn't
the case, then an object, by its definition in Lartraveran physics, would be a giant macromolecule with a single collective electron field,
and only individual molecules could have mass! At very, very low temperatures, it's possible to have a substance where its electron field radius
is higher than its square gressange, meaning you can have molecules without a single mass (this is one of the properties of nodolib state).
In permeate state, molecular bonds still hold molecules together, which means that matter in permeate state technically has mass, but only
the masses of the individual molecules rather than a product of the masses on the macroscopic scale, meaning its mass is microscopically low.
Chunks of ezzolmisated molecules are really just single giant molecules: a chunck of ezzolmisated matter has a single collective electron
field/molecular field, and the reason that ezzolmisation is a high-energy state is because the atoms need to have enough energy to be held
together by forces like magnetism even in a self-repulsive molecular field.
 Chapter 6: Consciousness and Time
Chapter 6: Consciousness and Time
Though the two-dimensional nature of Lartravera's planar time has been mentioned many times, so far I've sort of been taking it
for granted... so what does planar time actually mean, and how do lifeforms' consciousnesses interact with it?
What is Consciousness?
This is a question that has plagued science in our world since its very inception, and at this point the answer still isn't
entirely clear. In our world, consciousness from a scientific perspective is no more than an emergent property resulting from connections
between cells, and so the fact that us humans each experience the world ourselves rather than as a bunch of cells is a very curious thing that
we still don't fully understand. Since our understanding of consciousness in our world is so incomplete, I can't fully tell you about Lartraveran
consciousness either, but I can focus on a single element of it. Not only is there a scientific definition of an object in Lartraveran physics,
there's also a scientific definition of consciousness, though it's not quite as tight-knit: a consciousness is something that experiences time.
To be more precise, a consciousness has a perspective of time in which they exist in a certain area of time at once, and their position in time
moves in their perspective. A consciousness itself does not exist in space at all, only in time, but most consciousnesses (all that are known,
though it may be possible for there to be a consciousness that doesn't) inhabit a body, which does exist in space. A consciousness's body
doesn't actually travel through time with them and is just as susceptible to changing possibilities across time as the rest of Lartraveran matter,
so really a consciousness constantly inhabits different iterations of its body as it moves through time. Not all lifeforms inhabit bodies that are
single objects; a single unbroken gress-wave connection, which is what defines an object, is not required for a consciousness to inhabit a whole
body as opposed to just a part of it that is a single object, which means that single consciousnesses can emerge from connections of cells just like
in our world even if those cells are not close enough together to act as a single object. This can be taken a step further: there are certain
lifeforms in Lartravera that act like ant colonies/hiveminds in the sense that there are several bodies that all seem to act as one intelligence,
and indeed in some of these lifeforms there really is a single consciousness, in a single area in time from its perspective, that's inhabiting
multiple bodies at once. One of the least understood parts of Lartraveran consciousness, and indeed all of Lartravera, is memory.
Whereas a Lartraveran consciousness's perspective exists and moves within time and usually inhabits a body which exists in space, a consciousness's
memory seems to be independent from time and space. As you'd expect, a consciousness's memory can recall events in times that they've already seen
from their perspective... but how does this work scientifically? Memory in us humans comes from connections between neurons, but in Lartravera
memories can persist even when whatever material thing the consciousness emerges from (like neurons in our brain) is dramatically altered by the
possibilities of time. Consciousnesses in general seem to be something more incorporeal in Lartravera than in our world, and so the existence of
"souls" and consciousnesses without bodies is considered likely by many Lartraveran societies, whereas in our world these theories can (probably)
safely be disregarded as far as science is concerned.
Interactions Between Consciousnesses and the World Around Them
Part of the reason that Lartraveran consciousness is so hard to scientifically measure (not that consciousness is any easier to
scientifically measure in our world, of course) is that a Lartraveran lifeform cannot see or figure out the perspective of any consciousness
other than itself. Advanced civilizations have tools that can measure and map a consciousness's path through time, but you can't pinpoint their
perspective, as it's only possible for two consciousnesses to interact at areas in time in which their paths overlap. To a lifeform in Lartravera,
the actual perspectives of any consciousness other than themselves will always be unknown, and indeed it cannot be known whether they have a
perspective at all (solipsism is as valid of a theory in Lartravera as it is in our world). If you're a Lartraveran lifeform, then you'll probably
end up treating other people on the same path through time as yourself as if they have the same time perspective as you, while you'll probably
end up treating people on a different path through time as yourself as if they're not really people (in the sense of someone you can get to know)
but just parts of the events of time, as even if your paths in time overlap multiple times, the second time you see them, they'll have memories of
different possibilities than you do. Friendships forming between two people with different paths through time is not unheard of if those paths are
close enough, but it's very rare since they probably won't have the same memories of even equivalents of the same events. This is further
compounded by another realization: let's say the path through time of a particular consciousness is a straight line that's 3 seconds wide
(it goes on in length for a long time, but only 9 s2 is experienced at once). What about a point on the plane of time that's 10 seconds
away from the line? This consciousness's path through time does not include that point, but since it's not far away when it comes to distance of
possibilities, that lifeform probably exists at that point. This means that at different areas of time, there are different iterations of the same
lifeform, each with their own consciousness and thus their own memory, making it even more confusing to interact with lifeforms that aren't on the
same path as you because you might not even be talking to the same consciousness even if they're similar. Because Lartraveran lifeforms interact
with other consciousnesses only when their paths through time overlap, from the perspective of one lifeform, all other lifeforms effectively exist
at every point in their pathways through time at once (it's just that that one lifeform only gets to observe and interact with other lifeforms when
their pathways overlap), and some lifeforms believe that even their own perspectives are an illusion, and in truth all consciousnesses exist on
their entire time path at once.
I'm not sure about that last part, but I do know something else that's definitely an illusion in Lartraveran time: free will.
In Lartraveran time, all possibilities already exist on the plane of time, and thus any lifeform's actions and experiences are determined by their
path through time; to believe otherwise is to believe that the plane of time can be changed somehow, but changed over what? The only way that free
will could exist in Lartravera is if there was a third linear dimension of time over which the plane of time could change, and it could be argued
that this dimension of time is what consciousnesses travel down. Such a third dimension of time could explain strange concepts like how memory works,
but physicists across Lartravera have almost entirely ruled out such a possibility, as many of the laws of physics revolve around time in Lartravera
having two dimensions. There is, in fact, concrete proof that free will does not exist in Lartraveran time: as mentioned previously, there are
rare consciousnesses who have paths through time that loop back on themselves, and even if their memories allow them to remember the first time
they crossed a point in time, if they cross that point again they will take the same actions and see the same events as they did before.
All "change" only occurs with respect to time, and so the plane of time itself is unchanging. Though advanced civilizations have found ways to
bend and alter consciousnesses' paths through the plane of time, these points at which the paths change already exist and so the path of time was
already bent to begin with, and the action that bends the path will always happen because that's how time works.
Though lesser civilizations can live with the illusions, advanced civilizations have the methods to map out the plane of time to a pretty
significant distance from their current point in it, and in analyzing the map the illusions fall. In Lartraveran time, all possibilities are true,
which seems to imply that free will is more true than ever in Lartravera, but when you think about it hard enough, it becomes clear that since every
possibility is an existing point on the plane of time (and consciousnesses can't choose their path through time because to do so would require
another form of time separate from the plane of time to make the change over), the possibilities visited by a consciousness, including the choices
their body makes, are all determined by the areas of time their perspective visits, and thus free will cannot be true. The question of whether free
thought exists is still up for debate, but to answer that question would require me to confront what memory means and what the memories of
consciousnesses change over if it's not time (note that reversing direction in time does not result in lost memories), and that might lead back
into the discussion of a third dimension of time... and if I keep going down that rabbit hole, I'm going to end up like those cultists from the
planet Ritagnel who wholly believe that Lartravera secretly operates via threes rather than twos, using the fact that space is 3D as a base and
then coming up with theories like this consciousness dimension of time, a third type of matter that combines with the other two to form
consciousness instead of mass, and a third dimension of electricity that supposedly causes additional forces to account for quantum effects. I've
done enough research into Lartravera to know that these cultists are grasping at nonexistent straws, so we're going to move on before I have to
confront any of their obviously incorrect beliefs.
Perhaps some of these confusing truths and questions would be easier to answer if the "axis of causality and axis of possibility"
model was true (we could pretend that memory was gained on one of the axes specifically), but as I've said several times throughout this study,
that model of Lartraveran time is a simplification. But if the axial model is a simplification, then what's the true nature of Lartraveran time? It's
time to finally answer that question... but unfortunately not with one answer. The nature of time is even more of an enigma in Lartravera than
it is in our universe, so there are all sorts of different theories of time found in different Lartraveran societies. Out of all the theories I've seen,
three stand out as the ones that I believe are most likely to be correct, so I'll present all three here and leave some interpretation up to you.
The Uniform/Snapshot Model
Though the simplification I've been using up until now has around the same level of usefulness for all three of these models,
behind the scenes the model I've been using assumes that the plane of time is flat and uniform, with "uniform" here meaning that there are no points
or directions in time that are more important than any other on a universal scale. This model does not account for a beginning of the universe,
and assumes that the plane of time is infinite in all directions, which works because unlike in our universe, in Lartravera the universe doesn't
seem to always be expanding: it's been observed to both expand and contract, even on time directions that aren't opposites. Concepts like entropy
and the "arrow of time" are entirely subjective in this model, so it's up to each consciousness (or each society) to decide what direction in time
is "forward" and which directions are possibility directions, with the "forward" direction generally being assigned to whichever direction that
consciousness moves in the most. In this model, only consciousnesses actually experience and have paths through time. All particles, atoms,
molecules, objects, etc., including bodies inhabited by consciousnesses, only exist in individual points of time, and while there's the illusion
that they have movement through time, in reality every point in time is its own iteration of space, with only consciousnesses inhabiting multiple
times at once and travelling between them. This model can also be called the "snapshot" model of time, because it proposes that Lartraveran time
consists of an infinite number of infinitesimally separate snapshots, and consciousnesses are like observers looking through the snapshots from
particular perspectives. Still, even if the snapshot model is true and almost everything about Lartraveran physics is an illusion (space being 3D
and there being two types of matter wouldn't be illusions since those things are static, but just about everything else like mass, speed, forces,
and everything else that operates over time would be illusions), those illusions are still very useful so we shouldn't ignore them. After all,
for all we know, the "snapshot" model of time could be true in our world too, as unlikely as it feels.
The Radial Model
The uniform model is certainly one way to think about Lartraveran time, and even ignoring the snapshot part there's still
some facts about it (like how many consciousnesses have different definitions of what direction in time counts as the direction of
causality to them), but are there any useful theories that don't explain time away as an illusion? As it turns out, there are, and here's the
most popular theory that doesn't explain time away as an illusion: in the radial model of Lartraveran time, there actually is a point in time
at which the universe began, and all other directions in time spread out in a 360° range out from that point. Consciousnesses still have their
strange paths through time, but in this model their bodies travel with them, and non-living matter has paths in time as well. By default, all
matter moves in straight lines away from the origin, but all sorts of forces can influence their path, from the forces that keep matter held
together on the microscopic level (electrostatic forces, molecular magnetism, gress-waves, etc.) to forces acting on objects on the macroscopic
level. An object's motion through time obviously affects its motion through space, but in the radial model an object's motion through space also
affects its motion in time; the radial model of time is what was assumed to be correct as a basis of Delisha's Hypothesis and
Colinnnniss's Collorary, for example. In the radial model of time, the "direction of causality" is all directions that are moving directly
away from the origin, while moving perpendicular to the origin would be a direction of possibility, so in this sense there are in fact axes of
causality and possibility in the radial model, except the coordinates are polar rather than Cartesian. That's not all that's different about these
coordinates, though, as the geometry of the plane of time in the radial model isn't Euclidean, it's hyperbolic, as the amount of possibilities in
time grows exponentially the farther you go from the origin. This is also how the radial model accounts for how subjective the arrow of time appears
to be; it's not really subjective and properties like causality and the universe's expansion really do have a direction, that being straight away
from the center of time, but holonomy causes the perspectives of consciousnesses to become rotated in unexpected ways, so models of time that don't
account for holonomy result in an incorrect perception of causality... or so the radial model claims, of course. The plane of time has not
been observed to have a hyperbolic curvature by most Lartraveran civilizations (and those that have observed such a curvature may have had
their measurements interfered with by other things, such as an unaccounted-for curvature of space), but given it's unknown how large the plane
of time actually is, it's still unknown whether its curvature is actually zero or just appears to be from the scale of lifeforms.
The Spherical Model
The curvature of the plane of time is negative in the radial model, but if we're allowing for the possibility of this
then we should also consider a model in which the plane of time has positive curvature. Whereas the other two models assumed that the plane of
time is infinite and there's no limit to how large space can be, the spherical model of time assumes that the visible expansions and contractions
of space are just expansions and contractions of the observable universe (which might be true in the other two models too, if space is infinite),
and Lartravera as a whole is actually a single unchanging size. If the amount of space is finite,
so is the amount of possibilities that the universe as a whole can take, and so the plane of time is finite. The spherical model,
as you can guess, assumes that the plane of time is shaped like the surface of a very, very large sphere. The farther two points
on the sphere of time are, the more different the universe is at those points in time from each other, and points on opposite ends of the sphere
have pretty much everything in opposite states from each other, from position in the finite universe to types of matter to directions of events
and motions. Like in the uniform model, there are no defined axes of time, so directions of causality and possibility are subjective.
The positive curvature of time in this model naturally means that the pathways through time of consciousnesses intersect more than they would
if the plane of time was flat... but intersections can also come from another factor. In the spherical model of time, the plane
of time doesn't just have positive curvature: it's actually a sphere. The plane of time is still 2D, so there's no time and thus no matter or
events on the inside or outside of the sphere. However, the paths through time of consciousnesses work differently in this model
than in the other models: in the spherical model, consciousnesses take up a constant volume of time.
This could be measured in cubic seconds, though it would pretty much impossible to actually measure a consciousness's
volume in time even if the spherical model was true, as a consciousness only actually experiences the amount of area in their volume that
intersects the plane of time; the rest of their volume in time isn't consciously experienced, as there's no actual time to experience. This
gives a definition for unconsciousness: unconsciousness is when a consciousness's volume in time does not intersect the plane of time at all.
This means that when a consciousness is asleep, its perspective is moving through the interior or exterior of the sphere and thus the
consciousness wakes up in a different section of time. This also means that different iterations of the same lifeform are probably the same
consciousness, having traveled onto what appears to be a separate path but is actually the same path
after travelling outside of the plane of time.
There are, of course, many other theories of time in different places across Lartravera, such as theories that assume zero
(or positive) curvature but still give matter paths through time rather than just consciousnesses,
theories that don't set the curvature as constant and assume that the curvature of time varies at different points in time,
theories that unify space and time as a single 5D (or, depending on how they influence each other, even more dimensions)
concept and lay out interactions that this Lartraveran spacetime has with its components (we'll see more about this one soon),
and many, many more. That being said, I chose these three because they're the most-used theories throughout the universe of Lartravera.
The uniform/snapshot model seems to be the default (in the same way that Eulidean geometry is the default way of thinking about geometry for us),
the radial model is the most friendly for assumptions that link scientific concepts together (such as Delisha's Hypothesis) and so it's risen as the
most popular alternative to the uniform model, and the spherical model isn't nearly as well-known as the other two but it's still in third place
and it's the most "complete" model in the sense that it embraces phenomena that the other two models brush off as emergent properties or useful
illusions (though it's the least complete of the three in the sense that it has the least evidence; the radial model is more scientific, while the
spherical model is more conjectural). No civilization in Lartravera has reached a high enough point to confirm the true nature of time, so for now
all three of these models are still in the running... at least as far as an outside observer like myself can tell.
Grey Bit Computing
I mentioned the "grey bits" system of computing back in Chapter 1, but how does this really work? Bits can be used in two
contexts: as a continuous unit of probabilistic information, and as a quantized unit of information in a computer. Though the concept of
grey bits does have a use even in the probabilistic context, my research into Lartravera hasn't given me enough, well, information for me
to understand that concept... but I can explain how they work in a computer. In computers that use grey bit storage (or at least in the
models I've seen), each littra and darra bit is a single atom. In the example I'm using,
each bit atom is kept in a microscopic (size measured in some range of nanometers, probably) chamber that is split into two halves
at very different temperatures, and the computer uses the streggis and/or temperature of the gress-waves the atom releases
to measure which half of the chamber it's in and thus which state the bit is in. Each chamber is made of a group of molecules
that is littra-positive and darra-positive by default, but there are free electrons floating between the chambers that the computer's
mechanisms can force into or out of the walls of the chambers to switch the charges of the chamber halves and thus use electrostatic force
to move the bit atoms to the other half of the chamber, as the atoms used as bits are not electrically neutral elements. These chambers are
placed at distances that allow the bit atoms to form gressa with each other, and while the non-bit atoms will obviously participate in gressa
creation as well, by positioning the chambers correctly, keeping temperatures throughout the computer at particular values and using
ezzolmisation between bit atoms and non-bit atoms in the right way, the gressa atoms can be influenced to exist at particular locations
throughout the object. These computers have a bunch of additional chambers beyond the littra and darra bit chambers (One model I've seen is
like the multiplication table, with one matter's bit chambers on top, one matter's bit chambers on the left, and chambers for gressa atoms
along the rest of the square), and they have their internal conditions just right so that the gressa atoms created by interactions between
two bit atoms exist near these chambers while the other gressa atoms do not. Since gressa atoms are not true matter but emerge from littra and
darra's interactions, their existences can change position suddenly and pass right through solid matter, especially since gressa atoms aren't
really atoms: gressa atoms do not contain any particles, and while we still call them atoms because they emerge from atomic-level interactions,
they're actually more like single points of mass with zero or near-zero size. Because of this, grey bit chambers do not need to have
ranges of temperatures (that would be useless anyways, as mass is the only property that gressa has: no size, no temperature, no matter, no
charge, no energy, only mass... as far as I'm aware, anyways): they simply measure whether a gressa atom exists within the chamber or not
(which is arguably easier to do than for a littra or darra atom because, again, gressa has mass), and thanks to the strict configuration of the
computer, each gressa atom will in theory only be near one grey bit chamber. When data simply needs to be stored, the computer's mechanisms
decrease the temperatures and increase the charges of the littra and darra bit chambers to ensure that the atoms within them do not move and
thus the gressa atoms stay within their chambers... but often that's not enough. Thanks to the vast possibilities of time, even if the littra
and darra bits remain in the same positions, the gressa's positions can change slightly over time, causing some grey bits to be flipped.
In order to manipulate the grey bits without changing the littra and darra bits (which a computer needs to be able to do if we want it to be
able to manipulate individual grey bits and thus be able to use the grey bits for all the purposes computers use bits for), we need to use
this fact to our advantage. Advanced civilizations in Lartravera have found ways to measure events and possibilities in time to a very
precise degree, and so they can build computers powerful enough to calculate (using the littra and darra bits, since we're still in the
process of making the grey bits usable) the positions their grey bits would have at different points in time. Once it's been calculated what
nearby point in time and states of the littra and darra bits will result in the desired state of the grey bits (which, if we're only changing
a tiny fraction of the grey bits at once, which is almost always true given the sheer number of them, shouldn't be too far away in time), the
computer must travel to that point in time in order to get the grey bits into the desired position... but how does it do that?
Whether objects and matter even have paths through time is up for debate, but it's consistent through all theories of Lartraveran time that
consciousnesses do have paths through time. Therefore, these computers are created with additional bits, often using the more traditional
electrical computing since these ones aren't going to be involved in the grey bit process, arranged in a way that creates a neural-network-like
structure and thus an artificial consciousness made to be able to manipulate its own path through time (usually, the area of time this
consciousness occupies at once from its perspective is engineered to be very small so the time path calculations are precise). The computer's
consciousness calculates the desired position in time, travels to it, and sets the littra and darra bits into the previously calculated
states to result in the desired grey bit states, then it stores the states of the grey bits in its memory ("Memory" here means the conscious
definition of memory rather than the usual computer definition. Remember, Lartraveran consciousnesses' memories can somehow remember things
based on their own perspectives and semi-independently of their actual path through time) and returns to a point in time very close to the
point in time it began this grey bit-setting excursion from (it can't be the same point in time because otherwise its bit positions and values,
and indeed everything else, would be the same as before; the computer's consciousness's path through time can't really loop on itself
without risking failure), fine-tuning the bits as it travels back through time to retain the same states even at different points in time on
the way back because now it has the desired states in its memory. From the perspective of the computer's consciousness, this grey bit trip
may be quite long, but from the perspective of the user it only takes a moment for the computer to make its calculations. Grey bit computing
is only viable for very advanced civilizations, as it requires a very good understanding of exact specifics of temperature, gressa theory,
paths through time and how to manipulate them, and how to create consciousness. It's also a very unstable process since the method used to do
it (movement through time) is by its very nature uncertain and full of possibilities, so as mentioned previously, a lot of the bits are used
for backup and error-correction rather than actual calculations and storage. This "atom chambers" model isn't the only grey bit model of
computing I've seen, but no matter the specifics, inducing an artificial consciousness is the key to making grey bit computing work, and it's
also the key to the "time-tied" devices I mentioned back in Part 1: devices that are tied to a particular user to have the same path through
time as that user. The way these work is also by creating an artificial consciousness, with this one also adjusting its own path through time,
but in this case it's just to make sure its path through time is the same as that of its owner. For example, a time-tied electrical device
would have an artificial consciousness on the same path through time as its owner, and that device's consciousness would regulate its own
current to account for turns in the path, keeping up the illusion that the current is moving in one direction along the path of time.
Unconsciousness and Death
Let's end off this part by discussing an ending: what happens when a consciousness's path through time cuts off or ends?
I've already mentioned what unconsciousness means in the spherical model, but let's define it for all three models. No matter the theory of
time we're using, the general pattern is the same: as a consciousness falls asleep, the area of time they're experiencing at once shrinks,
and the consciousness officially becomes unconscious once that area hits zero. In the snapshot model, time sort of only exists from the
perspectives of consciousnesses, so when a consciousness falls unconscious, it's as if their perspective instantly jumps to the point in
time at which they become conscious again, though some have argued that unconscious lifeforms still have their perspectives moving through
time (even though they don't experience it) because there are still ways to measure a consciousness's path through time even through intervals
in their perspective where they're unconscious. In the radial model, the consciousness still moves along its path through time while
unconscious, but the width of their path along that interval of time is zero, so the area of time they're experiencing is zero, therefore
they're not experiencing anything, but their path through time remains continuous. As previously mentioned, unconsciousness in the
spherical model is when the volume of time the consciousness takes up at that moment in its perspective does not have any area intersecting
with the plane of time, and it wakes up once its volume travels to a position in which it has a cross-section with the plane of time again.
Unconsciousness is fairly easy to define at this point in my research (though we've had to discuss a lot of things
to get here), but what about the more permanent version? We treat death as a big mystery in our world, but from a purely scientific perspective
there's not much of a mystery: death is the point (well, it's more like a range of points, as the final process of dying is itself not
instantaneous and where the line is depends on your definition) at which your body irreversabily ceases to function. This definition
doesn't really work in Lartravera, though, as this definition relies on single-direction time. If we define death this way, then
since consciousnesses occupy a non-zero area of time at once rather than a single point, a lifeform could "die" on part of its
consciousness's path through time but still survive from the consciousness's perspective because a portion of its path did not
intersect the event where they died. Yes, this could be considered death as far as the events are concerned, but from the perspective of
the consciousness in question this is more of a near-death experience than an actual death. What happens when a consciousness's path
through time ends in full? This is a much better definition of death, but none of the three major models of time really accept that a
consciousness's path through time can just end. In our world, we have all sorts of unscientific theories on what happens after death,
and so do Lartraveran civilizations, though I have found some theories about what happens after death that are more scientific than others.
Since consciousnesses seem more incorporeal than their bodies in Lartravera, reincarnation in the form of "a consciousness without a
body drifts unconscious through time until it attaches to a new body and wakes up again" is a common theory seen throughout many
societies across Lartravera. Even those that believe that a consciousness can only exist in its own body point out that if a bodyless
consciousness drifts through time for long enough, it's bound to run into another iteration of its own body at a different point in time,
and this has spawned more theories, involving "reincarnation as another iteration of yourself" and "returning to an earlier point
in your life": these rely on the fact that memory can fade over time (this is true in our world too, obviously), and so if the consciousness
remains unconscious and bodyless for long enough from its perspective, when it wakes up again it will effectively be born anew. Others
believe that a consciousness doesn't actually need a body to have a non-zero area of experiencing time, which when you think about it
actually means they believe in ghosts. If a ghost is a consciousness that is awake (and thus exists in an area of time) but has no body,
then the question of what volume of space it's experiencing is up for debate: some believers in ghosts believe that a ghost would still
exist in a certain volume of space, while others believe that since they don't have a body to experience space, they sort of experience
all of space at once and yet none at the same time, which is probably a more scientific way to think about ghosts, but it isn't exactly easy
to comprehend or to write ghost stories about. Of course, there are also people that believe that a consciousness's path through time
really can just end. When it comes to theories of unconsciousness and death, the spherical model has one of my favorites: a
semi-scientific theory of an afterlife. Since a consciousness's volume of time remains constant no matter what, death in the spherical
model of time is best defined as a consciousness's volume of time drifting off into the space outside of the spherical plane of time
and never returning. If we assume that the consciousness still exists, then we can ask another question: what if there's a larger sphere
out there? If the sphere of time is on the inside of a larger sphere of time, then a consciousness drifting farther and farther away from
one sphere of time would eventually intersect this larger sphere, which would be like them entering a second universe of Lartravera in
which space and time are larger and there are more possibilities, but the laws of physics are the same (and even if they aren't all the
same, at the very least the laws of time must be the same). People who believe this usually assume that there are an infinite number of
these spheres, which also serves as an explanation for why no consciousnesses have been observed to appear from way over on the other side
of the sphere, which would go a long way towards confirming that time is spherical or at least looping in some way. There are simpler
explanations for this, such as "No civilization has the technology to measure time paths that long", "We can't measure paths through 3D
time even if they do exist because there are no events outside the plane of time", and "Memory loss would cause a consciousness coming
in from that far in time to effectively be reborn", but if the nested spheres theory is true, then a consciousness that goes too far
inside the sphere would intersect with a smaller sphere of time, a smaller universe. The nested spheres theory is a collorary to the
most unique of the major theories of time and it serves as an afterlife theory and a multiverse theory in one, and I think that's pretty cool.
While death can be defined as "the point in a consciousness's perspective at which they do not inhabit a living body at any point in the
area of time they are experiencing", the consequences of this definition have no single agreed-upon answer. Lartravera is a vast universe,
even larger than our own since time has an additional dimension, and so throughout its societies there are a nearly-uncountable amount of
theories about things as important as consciousness, time, and death, and I suspect there are some things about these concepts that
no Lartraveran will ever know for sure... but the presence of the word "never" in that sentence brings us right back to asking questions
about time, so we should probably move on before the rabbit hole widens once more.
 Chapter 7: Reality Fluctuations
Chapter 7: Reality Fluctuations
Lartraveran space is not entirely stable, and sometimes fluctuations occur within it. These distortions, these
fluctuations in reality, are very important to the true nature of Lartravera... to the point that we need a tenth base unit for them.
Chronovolume
We've seen space of possibilities in several places in Lartraveran physics thanks to its connections to forces and energy,
but what if we take volume of possibilities and multiply it by planar time instead of dividing? The resulting unit of
m3*s2 can be used to measure chronovolume, which has a few different meanings. Let's look at a hypothetical object
that always has a volume of 8 m3 and exists for 200 s2 in total, and its volume of possibilities in the average sense
(given a certain frame of reference) is 1,000 m3 over these 200 s2. If we use this volume of possibilities sense, then the
chronovolume of this object is 200,000 m3*s2, and this type of chronovolume can be used as a sort of measure of how varied
the existence of an object or consciousness is: an existence is more varied if it exists in more places over the course of its existence, and it's
also more varied if it exists for longer (even if it doesn't inhabit any more places) because it experiences more events. This, however, is not
the scientific definition of chronovolume. The scientific definition of chronovolume is best understood in the snapshot model of time, in which
each point in time effectively has its own 3D space. Under this way of thinking, we can't measure volume of possibilities over a non-zero
interval of planar time because such an interval contains an infinite amount of points of time in it (measuring volume of possibilities in a
standard sense assumes a frame of reference, such as positions in reference to a particular planet, and/or ignores the volume of the object itself
and treats the object as a single moving point in space so that the volume it takes up over an interval of time isn't infinite), so if we assume
that points in space at two different times are not actually the same point, then the amount of volume an object takes up over an interval of
time would be infinite. Since we can't measure volume of possibilities without a frame of reference when using this snapshot way of thinking,
we measure its chronovolume instead, which we do by taking its volume at each point in time and multiplying that by the amount of time it takes
up, so in the case of the object we used earlier, its chronovolume by the scientific definition is 1,600 m3*s2
(if the object's volume changes over time, we'll need integration to find the chronovolume). A useful, if hard to visualize, way to think about
chronovolume is this: rather than treating it as if each infinitesimal point on the plane of time has its own humongous 3D space within it,
we use five-dimensional spacetime, with three dimensions of space and two dimensions of time; the chronovolume of an object is the hypervolume
it takes up in this 5D spacetime. Visualizing a 4D hypervolume when dealing with spacetime in our world is hard enough, let alone a 5D hypervolume
for Lartraveran spacetime, but we'll need this notion of 5D spacetime hypervolume for the rest of this chapter. In particular, I'd like to note
that 5D spacetime is entirely static: since time is already incorporated into the 5D structure, there's nothing for it to change over.
If you could look at the entirety of the 5D spacetime at once, you'd see the entirety of Lartravera over all of space at every point and
interval of time, seeing all of history across the entire universe as a single unchanging and indeed unchangeable image.
There actually is a way to measure volume of possibilities without a frame of reference, but we're going to need some basic
calculus, so feel free to skip this paragraph if you need to; it's that 5D spacetime definition of chronovolume that we'll be using for future
paragraphs, so you don't need to read this paragraph if you haven't learned about integration yet. The fact that space of possibilities is
measured in m3/s2 is somewhat misleading, as space of possibilities in its most useful sense (instantaneous
space of possibilities) exists at a single point in time, not over an interval of time. Though macroscopic ways of approximately measuring space
of possibilities and volume of possibilities are often be dependent on frame of reference, the true internal value (the one that corresponds to
energy) of the space of possibilities of an object is not dependent on frame of reference. If we take the integral of this "internal" space of
possibilities with respect to an interval of planar time, we get a definition of volume of possibilities that is not dependent on frame of
reference. If we take the integral of this "internal" volume of possibilities, now we have a definition of chronovolume that does not rely on
frame of reference but also does not rely on the snapshot model of time or on 5D spacetime; this definition is a more formal version of the first
definition of chronovolume given in the previous paragraph, the "variety" definition of chronovolume. With that, we now have two definitions of
chronovolume, both of which are static and do not require a defined frame of reference to interpret. That being said, I'd say that internal
volume of possibilities is a closer measurement to spacetime chronovolume than variety chronovolume is, with the difference between the two
being that internal volume of possibilities treats the spacial volume of the object at a particular point in time as zero and looks at all the
locations that this single point (such as the object's center) exists at over an interval of time, while spacetime chronovolume takes the volume
of the object into account. Though variety chronovolume is an interesting concept, it isn't that useful for Lartraveran physics, whereas
spacetime chronovolume has some very important uses. Feel free to come up with other uses for variety chronovolume if you wish, but I'll
be focusing on spacetime chronovolume for this study.
Reality Fluctuations: The Basics
The reason it's useful to understand 5D spacetime and chronovolume is that Lartraveran spacetime
is not uniform. Some areas of spacetime are more unstable than others... and sometimes, this results in a reality fluctuation. From the
perspective of a consciousness moving through time observing a reality fluctuation from afar, a reality fluctuation is a bubble of
unstable space that starts at a point in space, expands to a certain volume, then contracts back into nothing. In reality, a reality fluctuation
isn't creating its own space, it's causing instability in the space already there and then the instability goes away. From the perspective of
static spacetime, of course, a reality fluctuation does not appear or disappear, it simply exists in a certain chronovolume of spacetime.
The chronovolumes of most natural reality fluctuations are hyperspherical (in the shape of a five-dimensional sphere), which means that from a
3D+2D perspective, a typical reality fluctuation occupies a circular area of time and a spherical volume of space, the spherical volume of space
it occupies is larger at points of time closer to the center of the temporal circle, and the circular area of time that it occupies a particular
point in space is larger for points closer to the center of the spacial sphere. What makes a reality fluctuation a reality fluctuation is
that spacetime is stretched and/or contracted inside it with a defined edge between the distorted spacetime and the standard spacetime;
if the density changes too gradually, it's not a reality fluctuation because there's nothing to measure the density relative to, so for all we
know there's no distortion. Only in the case of a sudden change in spacetime density can spacetime density really be measured to be different,
as spacetime density can only be measured relative to spacetime density in the surrounding area (the individual densities of space and time
can be measured relative to the other quantity, so you can measure the density of space in a particular volume of space at one point in time
relative to its density at another point in time, but since spacetime as a whole is static, its density can be assumed to be uniform
unless there's a clearly defined boundary of separation), and it's this sudden change that defines a reality fluctuation.
But what do "spacetime density" and its components of "spacial density" and "temporal density"
actually mean? This is where frame of reference comes back into play, because as previously mentioned, both spacetime density and its components
can only really be measured in reference to each other. In this case, the frame of reference we're using is the spacetime nearby to but outside
the reality fluctuation. Spacial density and temporal density are really just ratios measured in m3/m3 and
s2/s2 respectively, and therefore spacetime density would be measured in
(m3/s2)/(m3/s2) since spacetime density is the product of spacial density and temporal density;
1 m3/m3 is just the standard spacial density that the frame of reference you're using has, and likewise for the other two.
Let's look at some examples of how reality fluctuations distort spacetime. If we consider a reality fluctuation with a spacetime density of
32× (we don't actually need the units since all three of these densities are dimensionless) inside the fluctuation and we assume that the
stretching of spacetime is equal in all directions, then spacial density inside the fluctuation is 8× and temporal density inside the fluctuation
is 4× since there are three dimensions of space and two dimensions of time, and in general each of the five dimensions of space is stretched by 2×.
That last number is important, so we'll call that the "fluctuation factor" of the reality fluctuation, which in a reality fluctuation where the
stretching or compressing is equal in all directions will always be the fifth root of the spacetime density (and if it's not the fifth root
of the spacetime density, that means that the fluctuation factor isn't even in all directions). This means that if this reality fluctuation
has a diameter of 1 m at a given point in time from the perspective of a consciousness outside the reality fluctuation, then from the perspective
of a hypothetical consciousness inside the reality fluctuation, its diameter is 2 m because space inside the reality fluctuation is stretched to
twice its standard length. Similarly, if a hypothetical object (which we're assuming at the moment to be experiencing time but to only be
experiencing a single point in time at once, whereas consciousnesses are known to experience an area of time at once and objects are generally
assumed to not have paths through time at all) has a path through time that intersects the area of time in which the reality fluctuation exists
(but does not intersect the space in which it exists and thus does not actually intersect the reality fluctuation) for 1 s, then if that same
object with the same path through time is placed in the center of the reality fluctuation, from its new perspective the reality fluctuation exists
for 2 s because time is stretched to double its normal length. However, if a consciousness is experiencing 1 s2 at once outside the
reality fluctuation, then that same consciousness inside the fluctuation would experience 4 s2 at once since planar time is doubled in
two dimensions, and if the reality fluctuation has a volume of 1 m3 from the outside then it has a volume of 8 m3
from the inside since spacial volume is doubled in three dimensions. Finally, if the total chronovolume the reality fluctuation takes up is
1 m3*s2 from the outside, it's 32 m3*s2 from the inside. Of course, all of these numbers are for
a reality fluctuation where the spacetime density is 32× (and thus the fluctuation factor is 2×), and reality fluctuations come in all sorts
of different strengths: some stretch spacetime, some compress spacetime, some only stretch or compress space or time while leaving the other at
standard density, some stretch space and compress time or vice versa, and some stretch space and/or time in particular dimensions while
compressing them or leaving them unchanged in others. There's always five dimensions to work with here, and in most natural reality fluctuations
the stretching or compressing is uniform across all five, but these other varieties are still possible.
Measuring a Reality Fluctuation
Now that we know what reality fluctuations are - they're bubbles of spacetime that occupy a
certain chronovolume and have stretched and/or compressed spacetime within them - we can get to measuring them. We can measure the strength
of the effect of a reality fluctuation by multiplying its chronovolume by its spacetime density, so the unit of reality fluctuation effect would
be (m3*s2)2/(m3*s2) = m3*s2, which makes sense since spacetime density
uses a dimensionless unit so only the chronovolume unit remains, but keep in mind that reality fluctuation strength is offset from its
chronovolume by a factor of its spacetime density... well, sort of. A reality fluctuation with a spacetime density of 1 obviously has an effect of
0 m3*s2 because it's not a reality fluctuation at all, and because of the way that spacetime works, a reality fluctuation =
that compresses spacetime by a given factor requires the same fluctuation strength as a reality fluctuation that stretches spacetime by that
same factor, so what we're really multiplying the chronovolume by to get the strength is, say, (10abs(log(spacetime density)) - 1).
I like to call that function before the -1 the "multiplicative absolute value", and I'll be referring to the multiplicative absolute value of
spacetime density at least a couple more times in further discussion of reality fluctuations... but even the multiplicative absolute value of
spacetime density isn't quite what we have to multiply chronovolume by to get fluctuation strength. Using any functions other than multiplication
and division (and raising a unit to a numeric power, which is just repeated multiplication/division) on units
generally isn't allowed in dimensional analysis, and furthermore there's another factor to consider: a reality fluctuation of a given strength
can have a smaller or larger effect at some points in spacetime than others. For the most part, the less empty spacetime is in the hypervolume
in which the reality fluctuation forms, the weaker the reality fluctuation's effect will be. We know what space being less empty means,
it means there's more matter, but what about time? Time being less empty means that more events are happening: even if the universe was filled
with particles, if all of them were completely motionless, then time would effectively be a vacuum even though space would be far from a vacuum.
The more motion, the more collision, the more forces, the more energy, the more temperature and gress-waves, the more moving charges and other
electrical phenomena, and so on that are happening in an area of time, the less empty that area of time is. Taking both of these factors
(the fact that both stretching and compressing require fluctuation strength, and the fact that some areas of spacetime are more resistant
to fluctuation than others) into account, it's pretty clear that we're going to need a new base unit to measure reality fluctuations.
For this purpose, I will use the reliflux (rf), which is defined as "the fluctuation strength of a reality fluctuation that, in a complete
spacetime vacuum, would have an external chronovolume of 1 m3*s2 and a constant spacetime density of 2× inside it".
A complete spacetime vacuum does not exist in all of Lartravera, so any reality fluctuation will have at least slightly less of an effect
than in a spacetime vacuum, but when considering reality fluctuations in deep space, the factor by which they're weakened is pretty much
negligible. Now that we have a unit to measure them, we can look at some more facts about reality fluctuations. First of all, the relation between
fluctuation strength and chronovolume is intuitive: if we keep the spacetime density constant, then the higher the fluctuation strength,
the larger the chronovolume of the reality fluctuation. This is a direct relationship, so if we want a 2× spacetime density reality fluctuation
to have an external chronovolume of 2 m3*s2 in a spacetime vacuum, we'll need 2 rf of fluctuation strength. The relationship
between fluctuation strength and spacetime density is more complicated, as the amount of resistance spacetime gives towards being stretched
or compressed increases the more it's stretched or compressed, and so the fluctuation strength required to increase the multiplicative
absolute value of the spacetime density increases by the square of said multiplicative absolute value. To be specific, the fluctuation strength
required for a reality fluctuation with an external chronovolume of 1 m3*s2 and a spacetime density of N× (or ÷N) where N
is above 1 is (N2-1)÷3. This means that if we need 1 rf for a spacetime density of 2× or ÷2, then we need 2⅔ rf for 3× or ÷3,
5 rf for 4× or ÷4, 8 rf for 5× or ÷5, 5/12 rf for 1.5× or ÷1.5, and so on.
We can also derive units for the resistance that spacetime gives towards fluctuations:
we could measure this as a ratio in rf/rf (reliflux required for a reality fluctuation with a given effect in this area of spacetime
/reliflux required for a reality fluctuation with the same effect but in a spacetime vacuum), but we could also attempt a definition
using other units by measuring the amount of fluctuation strength required to achieve a given fluctuation effect. Since
fluctuation strength = chronovolume * ((10abs(log(spacetime density)))2 - 1) ÷ 3 * spacetime resistance
(if we assume that a vacuum has a spacetime resistance of 1), spacetime resistance could be measured in
rf/(m3*s2)/((10abs(log(m3*s2/m3/s2))) * 2 - 1) × 3, which is certainly
a weird unit. This certainly isn't valid as a standard derived unit (though I suppose it's no less valid than using decibels for sound,
as those are also logarithmic), and personally I'd like to have a more clean definition. To do that, let's get rid of that
non-standard part; not by redefining the laws of physics, I can't do that, but by redefining the unit definition. If we divide fluctuation
strength by chronovolume, we're left with a unit that essentially measures the fluctuation strength at a single point in space-time, which
I'm going to call the "distortion force" at that point. The actual effect that distortion force has on spacetime density varies based on
spacetime resistance, so if we divide that out too, we're left with that nonstandard part of the unit,
((10abs(log(spacetime density)))2 - 1) ÷ 3, and so we can clean things up by defining that as a unit itself.
I'm calling this unit the drezzitch (dz), and it measures "distortion energy", which measures how strong the distortion in spacetime at
a particular point is. The drezzitch actually makes more sense to use in the definition of the reliflux than spacetime density does: if spacetime
is stretched in three dimensions by 2× but contracted in the other two dimensions by 2×, then its spacetime density is 8/4 = 2×, but since
stretches and contractions by the same factor require equal fluctuation strength, the fluctuation strength acts as if spacetime density is 32×;
the stretches and contractions compound rather than cancelling, and distortion energy accounts for this. This means that using just spacetime
density can result in an incorrect reliflux measurement, but if we let distortion energy stand as its own concept rather than defining it by
the formula (though the formula still applies if the spacetime distortion is uniform), then the error goes away. The reliflux is now defined as
"the fluctuation strength of a reality fluctuation that, in a complete spacetime vacuum, would have an external chronovolume of
1 m3*s2 and a distortion energy of 1 dz at all points inside it". Since we're defining the drezzitch on its own now
(it's definition could be "the distortion energy that results in a spacetime density of 2× when applied uniformly across a reality fluctuation"),
we definitely have a new base unit on our hands, whether that be the drezzitch or the reliflux. The drezzitch could be defined as the base unit,
but I prefer to make the reliflux the base unit. If we then define spacetime resistance as rf/rf, we can define 1 dz as
1 rf/(m3*s2)/(rf/rf). The unit for distortion energy is dz, the unit for spacetime resistance is rf/rf,
the unit for distortion force is dz*rf/rf (which I'm going to call "df") and the reliflux itself is equal to
1 df*m3*s2 = 1 dz*m3*s2*rf/rf (yes, that's defining a unit in terms of itself,
which is why the reliflux should be the base unit so we don't have to define it this way. Then again, dz/dz works just as well as rf/rf
as a unit for spacetime resistance, so we could make the drezzitch the base unit and define 1 rf as 1 dz*m3*s2*dz/dz).
Making the reliflux the base unit but still defining it in terms of the drezzitch isn't unprecedented; after all, in the actual metric system,
the meter is defined using m/s, the kilogram is defined using J*s, the kelvin is defined using J/K,
the ampere is defined using the coulomb, and so on.
There are other units we can derive from the reliflux and reality fluctuations, of course.
Like in our universe, some particularly massive cosmic objects can collapse into singularities, but unlike in our world,
Lartraveran singularities usually create reality fluctuations instead of black holes, and these fluctuations
often aren't hyperspherical: thanks to the singularity generating a constant distortion force, they often take hypercylindrical
(the spacial volume of the fluctuation is the same at all, or at least almost all, of the points in time at which it exists) or hyperconical
(the spacial volume of the fluctuation and the cross-sectional length of time it exists across starts at a maximum when the singularity forms
and both decrease as you move in time away from that point, and at the end of the fluctuation's existence its volume and the cross-sectional time
it exists in approach zero) shapes, and as such it makes sense to measure the strength of a reality fluctuation at a particular point in time
rather than as a whole. This would be measured in rf/s2, a unit called the Dentali (Dn), which is equal to 1 dz*m3*rf/rf,
and in a reality fluctuation with constant distortion force in constant spacetime resistance, the single-time fluctuation strength,
which I'm calling "dissatus" (a portmanteau of "distortion" and "status", as it's basically the status of the reality fluctuation at
a single point in time), is directly proportional to the volume of the reality fluctuation. Similarly, we can use
rf/m3 = dz*s2*rf/rf to get a unit that's proportional to the interval of planar time in which a reality fluctuation
includes a particular point in space, i.e. the fluctuation strength at a single point in space, a unit which isn't given a name in
as many Lartraveran civilizations as the fluctuation strength at a single point in time is (the Dentali was named for a scientist in one of
Lartravera's civilizations, and the same goes for units like the Neotow and the Kristine; of course, different Lartraveran civilizations
have different names for units of the same dimensionality, but in these cases I'm using the names given to these kinds of units from one of
the most prosperous civilizations in the universe).
Quantum Reality Fluctuations
It takes an extremely precise distortion force measuring device to confirm this, so precise that skeptics can easily
brush off these measurements as inaccurate, but measurements taken by the scientists from the most advanced of Lartravera's civilizations
seem to agree that Lartravera is in constant fluctuation at subatomic scales. If these measurements are accurate, then tiny reality fluctuations
with volumes smaller than the smallest particles of matter and equally tiny lifespans (areas of time) are constantly appearing and disappearing
across all of Lartravera; in terms of spacetime, this means the chronovolume of unchanging spacetime is dotted with tiny fluctuations across
its entirety. If this is true, then could we measure the average fluctuation strength across a given chronovolume of spacetime? Well,
the fluctuation strength on average of these tiny fluctuations could be measured, and there's some useful info to gleam from this: areas
of spacetime with higher spacetime resistance have a higher density of these "quantum reality fluctuations"
(so there are more quantum reality fluctuations on average per unit of chronovolume... while we're at it, I should probably give a name to the
unit of chronovolume. The name I've chosen is the "sequinter"; you can refer to the sequinter with a symbol of sq if you wish, but I'll
keep using m3*s2 so readers don't lose track of what chronovolume actually is), which seems counterintuitive at first,
but this increased density of quantum reality fluctuations is actually what causes spacetime resistance: when there are more
quantum reality fluctuations per sequinter, there's less room for a single reality fluctuation to expand onto non-quantum scales,
so more distortion force and thus more fluctuation strength is required for a reality fluctuation of the same distortion energy, which is
what spacetime resistance means. We can't measure average fluctuation strength as a whole over a chronovolume of spacetime because
fluctuation strength is a unit that by definition exists over a chronovolume, so what we'd be measuring in this case is total fluctuation
strength over that chronovolume, not average fluctuation strength. However, we can divide out that chronovolume, and doing so gets us
a measure of the average distortion force over that chronovolume. We can also measure the average dissatus across a particular volume of space
(this would be measured in Dentali, but in this context the unit is often called the Avinel (Av) instead even though it's just
a measure of the average of the Dentali measurements across the volume of space) or the average single-space fluctuation strength across
a particular area of time. Properties of the surrounding spacetime like the presence of matter and events can increase or decrease the
average quantum distortion force (which is still in the unit of distortion force, but that unit is often represented by χ instead of df
when referring to average quantum distortion force), both by changing spacetime resistance and via other effects. In particular,
the energy of the surrounding matter can have a strong effect on average quantum distortion force. When traveling over very long distances,
matter experiences a sort of friction or drag force from space itself (this is caused by quantum reality fluctuations), causing some of the
matter's energy to be lost to space. Even though this more of a drag force than a friction force, it's generally referred to as "cosmic friction".
The energy lost to space from cosmic friction then becomes fluctuation strength (but the process isn't directly proportional,
so we can't measure fluctuation strength in Kristines. There still is a proportionality to it in that a given amount of energy converted into
fluctuation strength across the same amount of time always results in the same amount of fluctuation strength, but the longer it takes for the
energy to be converted, the more of it is retained as fluctuation strength), which usually results in an increase in average
quantum distortion force. Therefore, average quantum distortion energy and average quantum distortion force are variable based on the energy
of the surrounding matter.
Stable Quantum Reality Fluctuations
Reality fluctuations are unstable in nature. Unless something like a singularity or transfers of energy into distortion
energy via cosmic friction is keeping the fluctuation going, a typical reality fluctuation only occupies a small chronovolume and its
spacial volume decreases as you go farther from the center of its temporal area. This is especially true for quantum reality fluctuations,
as their chronovolume is tiny but they often have a very high amount of distortion energy during their brief existence... but what if they
weren't so unstable? What if a quantum reality fluctuation could take a shape with a macroscopic temporal area and a constant, if still
microscopic spacial volume? If this was possible, such a reality fluctuation wouldn't appear to macroscopic lifeforms like a reality
fluctuation at all... it would look like a subatomic particle of matter. This might sound crazy, but one of the most curious yet plausible
theories I've seen of what matter in Lartravera actually is is that there are certain configurations of distortion energy/spacetime density,
distortion force, and spacial volume in a quantum reality fluctuation that result in it being stabilized in this way, and that all matter is,
on the quantum scale, actually these reality fluctuations, with each different stable combination corresponding to a different subatomic particle.
The theory holds that the difference between littra and darra is that one of the matter types corresponds to stable quantum reality fluctuations
(SQRFs) with spacetime densities above 1, while the other matter type corresponds to SQRFs with spacetime densities below 1,
and charge is based on the uniformity of the fluctuation: an SQRF with uniform distortion energy across its interior has no charge,
while SQRFs with non-uniform distortion energy do have charge: the distortion energy is greater towards the center of the SQRF in
positively-charged particles, while the distortion energy is greater towards the edge of the SQRF in negatively-charged particles.
SQRF theory posits that mass is a property of the distortion force interactions between expansion SQRFs (spacetime density above 1)
and compression SQRFs (spacetime density below 1) rather than a property of an emergent "third type of matter",
so gressa theory (as it's commonly understood, anyways), is incompatible with SQRF theory. SQRF theory is controversial,
even among the civilization that came up with it, for a number of reasons, the most important of which is that if SQRF theory is true,
then littra-darra symmetry (the principle that the universe would be fundamentally identical if all of the littra was replaced with darra
and all of the darra was replaced with littra, and such a universe would be indistinguishable from the real Lartravera) would not apply
on the quantum level; the same goes for charge synergy and several other symmetries of physics, but littra-darra synergy is by far the
most important synergy of Lartraveran physics. If SQRF theory is true, then there's a lot of things that most Lartraveran scientists have
thought to be true that will have to be reevaluated... but there are also some important properties of matter and space in Lartravera
that are best explained by SQRF theory, and you'll get to learn those throughout some of the rest of this analysis.
How Civilizations Use Reality Fluctuations
SQRF theory aside, what uses do Lartraveran civilizations have for reality fluctuations?
The most obvious uses for reality fluctuations come from their defining characteristic of having a different spacetime density on the inside
than the surrounding spacetime. Lartraveran scientists that have technology capable of inducing reality fluctuations can use
expansion fluctuations as a tool for simulating large-scale events within a small external volume of space, because inside the reality
fluctuation there literally is more space. The same goes for time: scientists can use expansion fluctuations to simulate events that happen
over large timescales within much shorter ones, as time passes faster within the reality fluctuation than it does on the outside. Conversely,
compression fluctuations can be used to simulate events that happen on smaller scales, both in space and in time. If you have something
very large you want to store, you can use a compression fluctuation to compress it to a smaller size; this works because when matter enters a
reality fluctuation, the distance between the molecules (or, in substances with strong enough links between their parts, it can be
the distance between larger sections than molecules) changes because of the change in the amount of space, so putting something large
in a compression fluctuation can literally shrink it down to a smaller size, then when it leaves the fluctuation it will return to its
normal size. On the other hand, if you have a container that's tight enough to hold its shape even as space changes density around it
(ezzolmisating the container is a good way to do this), then you can use an expansion fluctuation for storage instead: since the objects
that enter the fluctuation won't expand if they're in these containers, there will be more space to store them due to the nature of
expansion fluctuations. This means that both types of reality fluctuations can serve as storage spaces
(compression fluctuations by temporarily shrinking the object, expansion fluctuations by being bigger on the inside), but the
expansion fluctuation method is more reliable, as compressing the matter in an object can lead to it breaking, causing unwanted reactions
within the object, or otherwise ceasing to function as intended, whereas with the expansion fluctuation method, the objects themselves remain
the same size, not to mention that the compression fluctuation method requires the fluctuation's external size to be at least as large as the
object(s) being stored, while for the expansion fluctuation method it's the internal size that matters. There's also uses for
expansion fluctuations without the ezzolmisated containers and compression fluctuations with them: putting a small machine into an
expansion fluctuation can make altering intricate parts of the machine easier since they're expanded to a larger size
(the physical altering of the parts would have to be done with mechanical arms, drones, etc., but precisely using such machines is child's play
to a civilization advanced enough to create and sustain their own reality fluctuations), while a large compression fluctuation can be used as
a method of quick transport of materials by literally shrinking the amount of space the transport vehicle needs to travel through to get to
their destination (such "compression fluctuation highways" are the closest thing Lartravera has to wormholes, at least as far as I'm aware).
The list of uses an advanced civilization in Lartravera could have for reality fluctuations goes on and on, and these are just a few examples.
It's also possible, though very unlikely naturally, for a reality fluctuation to form inside another reality fluctuation, and while
I can't think of any particular uses a civilization would have for nested reality fluctuations, I'm sure that such uses do exist.
The most fantastical use of reality fluctuations is their ability to transform matter.
A reality fluctuation's border isn't really instantaneous, it's near-instantaneous, and often the distortion energy within the
tiny thickness of the border is stronger than within the reality fluctuation's interior (if the distortion energy at the edge is weaker
than within the interior, it's probably not an official reality fluctuation at all, just a barrierless distortion in space that fades in
around a certain chronovolume of spacetime). If the border of a reality fluctuation is powerful enough ("powerful" meaning a more sudden
change in distortion energy: both decreasing the thickness of the border (measured in meters) and increasing the distortion energy across
the points on the border (measured in drezzitch) increases this power, meaning that fluctuation border power can be measured in dz/m),
then matter crossing the border can be torn apart or crushed together by the sudden changes in spacetime density. Not only can this tear
apart molecules and atoms, but beyond a certain critical point, even fundamental subatomic particles will be unable to keep themselves together
(this point is the "particle distortion decoherence constant" or just the "decoherence constant", measured in units of dz/m.
The decoherence constant is different for different fundamental particles, and SQRF theory posits that the decoherence constant for
a given fundamental particle is based on the properties of the reality fluctuation inside that particle), and what happens after that depends on
the nature of the reality fluctuation that the particle is entering or exiting. In most natural cases, matter that crosses a
matter-decohering fluctuation barrier is turned into further spacetime distortion, which increases the fluctuation strength of the
reality fluctuation (i.e. alters the spacetime density inside the fluctuation and/or makes its chronovolume larger than it would have been without
this conversion). By bombarding a matter-decohering fluctuation with matter, advanced civilizations can convert the matter into strengthening
in the fluctuation, which can in turn be converted into actual energy by a process that acts as the reverse of cosmic friction
(remember, all processes in Lartravera are reversible thanks to the nonlinear nature of time), which gives advanced civilizations
a method of energy generation that converts all of the matter used into energy at maximum efficiency,
as matter-antimatter annihilation does in our world (it should be obvious that matter-antimatter annihilation can't be used as
a power source in Lartravera). However, if the power of the fluctuation border is almost exactly at the decoherence constant,
then the matter might not be converted into distortion energy: instead, it will lose its identity just enough that the particles will be
transformed into other particles instead. The exact rules behind how particles transform when crossing decoherence-point barriers
are beyond my comprehension, but there's one particular use of this that's caught my attention. While natural reality fluctuations
usually take a hyperspherical chronovolume shape, advanced civilizations can create reality fluctuations in all sorts of shapes and fashions.
For one particular use, a reality fluctuation's collapse is controlled so that instead of shrinking in spacial volume, its volume remains constant
but the distortion energy across each of its points smoothly decreases to zero; in other words, the fluctuation is made to fade away
instead of collapsing. If a compression fluctuation with a decoherence-point barrier (which itself must be specifically maintained during
most of the fading, as otherwise the barrier's distortion energy will also decrease and it will no longer be matter-decohering) and filled
with matter is made to fade away like this and it's bombarded with matter at just the right intervals, then as the fluctuation's
spacetime density smoothly returns to 1 (relative to the surrounding spacetime, of course), the distance between the particles of matter
inside the fluctuation will not increase: instead, the matter that enters the fluctuation will occupy the space at the edge of the
fluctuation's interior, and the entering matter will be transformed into a copy of the matter already inside the fluctuation
(the space-occupying part can happen even with a weaker barrier, but the transformation only happens when the barrier is at the decoherence point;
this works because the decoherence points of the particles that most of Lartravera is actually made of (the equivalents of our world's up quarks,
down quarks, and electrons, as those are the three fundamental particles that almost all matter in our world is made of,
though in Lartravera it may be the case that protons and neutrons are fundamental particles and there's no equivalent to quarks;
I'm not sure about that part) are identical to each other). For example, if you have a block of copper (or whatever the Lartraveran equivalent is,
since molecules require both matter types to form) that contains 25 kg of matter, and you set up a machine to bombard such a fading and
transforming reality fluctuation (which I'm going to call a transforma-fade flucutuation) with 75 kg of matter at just the right times
and intervals, then regardless of what that matter was before it entered the fluctuation, after the fluctuation fades, you'll have
three new identical copies of that copper block (for a total of four copies of the block counting the original, since it'll be impossible
to tell them apart) because the transforma-fade fluctuation transformed the entering matter into copies of the block.
Transforming matter like this has all sorts of uses, the most obvious of which is mass-production: for example, if an advanced civilization
has some very complex microchip or something like that, then instead of going through all the steps of programming a machine to
create these microchips, they can put the microchip in a transforma-fade fluctuation and program a machine to control the bombardment of the
fluctuation with matter at the right intervals for decoherence copying, and just like that they've got a bunch of identical copies
of the microchip. The more compression of spacetime that they can get inside the fluctuation, the more precise they can be with what gets
copied this way, and the more copies they can make (because the space inside the fluctuation expands more as the fluctuation fades if
the compression starts out greater) with a single fluctuation. Using those rules of matter-transforming (which I don't understand in full)
and controlling the barrier power of the fluctuation, an advanced civilization can program their matter-bombardment machines' intervals
to control the levels of bombardment so that some matter is transformed and other matter remains the same, with that other matter now being
inside the fluctuation and thus becoming part of what's being copied by the matter that is being transformed. If an advanced civilization
can create a transforma-fade fluctuation that compresses spacetime down to the molecular scale, then using these bombardment machines they can
turn an entire chunk of matter (like, say, a rock) into purely that molecule, or even into an exact mixture of molecules by using
selective transformation intervals. If the compression compresses spacetime down to the atomic scale, then they can freely edit every single atom
within the chunk of matter as long as they have at least one atom of each element they want to use, which can include creating whatever molecules
they wish within it. And if spacetime is compressed down to the level of fundamental particles? The advanced civilization would essentially
be able to edit everything about that clump of matter down to its most fundamental level, bypassing every property the matter once had
and transforming it into anything they want; by converting distortion energy within the fluctuation into matter as it fades,
they could even bypass the conservation of the amount of matter, allowing them to turn a single particle into anything they want,
no matter how large (as long as it's not larger than the external size of the fluctuation). With a transforma-fade fluctuation of
that kind of power, such a civilization would be godlike in power...
...but they wouldn't have every godlike power. Near-omnipotence, sure, and since they could
create anything using these fluctuations they could learn almost everything about almost everything and achieve near-omniscience,
but definitely not omnipresence. There's a reason why interacting with matter inside a reality fluctuation requires machinery,
and it's not just because some of the processes are too complex to do by hand. Reality fluctuations repel consciousnesses:
when a consciousness gets too close to a reality fluctuation, the consciousness's path through spacetime is repelled from the fluctuation.
The consciousness's body will not experience this repulsion, so the spacial part of the repulsion may not actually push the consciousness
since it's tied to its body, but the temporal part of the repulsion will. This means that creating a reality fluctuation is a way for
doctors to change a patient's pathway through time if the patient really wants it to change; for civilizations that don't have the technology
and/or understanding to create reality fluctuations, the alternative is a surgery where the doctor goes in and moves the patient's neurons
(or their equivalent to neurons), as this can also alter their path through time. Whether using neural surgery or inducing a fluctuation,
doctors can change a patient's path through time to a particular path they want to have if they know what they're doing,
but deciding to change your path through time is not an easy decision. Even ignoring the material costs of doing so
(in civilizations that do have a currency, a temporal movement surgery is probably extremely expensive, and even the
fluctuation inducing method must be done with precision), changing your path through time usually means losing touch with all of your friends
and family you've made up to that point, as their paths through time will no longer line up with yours and you'll drift apart in time from them
(Unless, of course, they're all having the same time path change done too, perhaps as a way to escape some terrible future such as an apocalypse).
The spacial part of reality fluctuation repulsion isn't without an effect either: the strength of the repulsion
(it's not a repulsive force, per say, as it's applied to consciousnesses themselves (NOT their bodies) and since a consciousness isn't a
physical thing you can't apply a force to it, but it is a repulsion) is based on distance to the edge of the reality fluctuation
rather than the center, and so it's impossible for a consciousness to actually cross the border of a reality fluctuation
(but this is only true if it would be crossing the border across the entire area of time it's occupying at once; a consciousness and its body
can move in such a way where it looks like the consciousness is crossing the border of a reality fluctuation, but it's not actually doing so
because the points in spacetime it's standing at aren't actually intersecting the chronovolume of the fluctuation, it just looks like it
from the perspective of another consciousness looking at the one near the fluctuation. Depending on a lifeform's tolerance to this repulsion,
it could even stick one of its appendages into the fluctuation; it's only impossible for the consciousness itself,
(which would located in the brain for us humans, for example) to cross the barrier). As a consciousness nears a reality fluctuation,
the spacial repulsion will cause it to feel something similar to a temporal headache (the feeling a lifeform gets when their area of time
contains a sudden-change event like a car crash, and they're experiencing both a split-second before the crash and a split-second after the
crash at once), but this feeling lasts longer. This "headache" is actually spacial rather than temporal, as the consciousness is
subconsciously struggling to remain tied to its body. If a consciousness gets too close to a reality fluctuation, the repulsion will
overpower the consciousness's tie to its body, and the consciousness will be pushed out of its body. Since a consciousness only exists
because of the brain (or equivalent to a brain) that's causing it, it's generally held that the consciousness dies when this happens,
but of course there are always those that believe in ghosts or the spherical model of time or some other theory that doesn't believe a
consciousness needs a body to exist, so it can't be said for sure what happens to a consciousness when it is expelled from its body in this way.
For most lifeforms, fluctuation repulsion occurs even while they're unconscious, but a small fraction of lifeforms across Lartravera do have
the ability to cross reality fluctuation borders while unconscious (but they'll still experience fluctuation repulsion while conscious),
and for these lifeforms reality fluctuations have even more uses... but it's debatable whether these lifeforms are even conscious, as it's
been universally shown that lifeforms capable of crossing reality fluctuation borders while unconscious do not have other properties of
consciousness: for example, their memories are completely physical and thus subject to the whims of time, whereas most consciousnesses can
retain their memories even if they end up looping back on a point of time they've already been at.
Difluctuation Repulsion
Reality fluctuations don't just repel consciousnesses: they also repel each other sometimes.
Two reality fluctuations will normally have no effect on each other as they approach each other, until they reach a certain spacetime distance
from each other and suddenly they repel each other, a phenomenon I'm going to call "difluctuation repulsion". This repulsion actually
is a force and can thus be measured in Neotows, but unlike most repulsive forces, it does not get stronger as the two fluctuations get
closer to each other, so if you can push two reality fluctuations together and overcome their repulsion once it activates, then you can
get them to collide, but if you don't push hard enough to overcome the repulsion then the two will remain at an equilibrium distance,
the distance where the repulsion would activate if the reality fluctuations got any closer. SQPF theory posits that this principle of fluctuation
equilibrium distance explains properties like the sizes of atomic nuclei, proton fields, and the distances at which electrons orbit the nucleus
of an atom: if all subatomic particles are actually SQRFs, then difluctuation repulsion applies to them too, so the distance that electrons
orbit an atomic nucleus is based on their equilibrium distances from each other and the nucleons. Because difluctuation repulsion doesn't
change strength based on distance, it can only be on or off, but the trick is that the force seems to apply across an area of time at once
based on the chronovolumes of the reality fluctuations, so the strength of difluctuation repulsion between two reality fluctuations
when it's active is based on their entire fluctuation strengths (measured in rf) rather than their dissatuses (which would be measured in Dn).
To be specific, difluctuation repulsion strength is based on the product of the fluctuation strengths of the two reality fluctuations,
so difluctuation repulsion strength can also be measured in rf2, and the force of difluctuation repulsion per square reliflux
(measured in No/rf2) is a universal constant of Lartraveran physics. The distance at which difluctuation repulsion activates,
on the other hand, is based on several factors, the most important of which is the strengths of the barriers of the reality fluctuations
in question.
Usually, the force of difluctuation repulsion is measured in force units like the Neotow,
but difluctuation repulsion may be linked to "diflux waves", which are similar to gress-waves in that we can't really detect them,
they're mostly theoretical, and calling them "waves" is somewhat inaccurate as they're a way to represent the interaction between the two
reality fluctuations and aren't quite physical things. The strength of diflux waves can be expressed in rf2, and the location in
spacetime that a diflux wave occupies is based on the positions of the reality fluctuations that are generating the diflux wave. Though a
diflux wave does not increase in strength as the reality fluctuations grow closer to each other, its motion does become more pronounced;
diflux waves are sort of moving away from the reality fluctuations creating them, but they're not really moving if the reality fluctuations
creating them don't move: it's as if they're always in a state of moving away from the fluctuations without actually moving away.
This "motion" is faster the closer the fluctuations are to each other (until the two reality fluctuations actually touch, at which point they
merge into a single stronger fluctuation and the diflux waves disappear). Diflux waves are also curious in that they seem to have no effect
on the rest of the universe at all; diflux waves can be affected by reality fluctuations and by all sorts of other things, but diflux waves
themselves have no effect on the universe at all, or at least no effect that I know of; two diflux waves won't even interact with each other,
they'll just pass right through each other (in contrast, gress-waves are responsible for both the creation of gressa and temperature
equilibrium if gressa theory is correct). This noninteraction is why diflux waves are theoretical and probably always be
(if they don't interact with the rest of the universe, how can it be proven they exist?), but they can still be measured (in theory) by measuring
the difluctuation repulsion of the two reality fluctuations creating them (though we can't really confirm they exist, so all we can do here is
measure the difluctuation repulsion and know what the diflux waves from that would be like if diflux waves do exist). However,
sometimes measurements of diflux waves return multiple results at once, and when combining this with the fact that diflux repulsion acts across
an area of time, it appears that diflux waves have paths through time like consciousnesses do. Like consciousnesses, these paths through time
can loop on themselves, and since a diflux wave usually occupies much less temporal area than a consciousness's total existence because the
reality fluctuations creating the diflux wave soon return to equilibrium distance (at which diflux waves do not form), their supposed paths
through time loop on themselves more often than consciousness's paths through time do, as for most consciousnesses their paths through time
will not include many (if any) loops. Whereas everything else in the universe, from matter to energy to events, will always be the same
and happen in the same way when a consciousness visits the same point in time twice, the consciousness's memory may not be the same...
and if diflux waves do have consciousness-like paths through time, then the fact that a single measurement of diflux wave strength can return
multiple answers may be explained by diflux waves also being able to have different states at different points in time like a
consciousness's memory does (this doesn't violate the rules of time because of the aforementioned noninteraction between diflux waves
and everything else, so diflux waves having different strengths at the same point in time will have no effect on the events that happen
at that time). The equilibrium distance of two reality fluctuations isn't just dependent on their fluctuation strengths: factors like
spacetime resistance and surrounding matter, energy, distortion energy in the case of nested fluctuations, events, etc. all play a role.
In particular, when two reality fluctuations are within some other material, some materials have a higher "difluctuation conductivity"
(which would probably be measured in a unit like m/rf2) than others, meaning that difluctuation repulsion can occur at larger
distances between the two reality fluctuations (materials with a higher difluctuation conductivity are also better at carrying diflux waves,
which means that if diflux waves do have paths through time, the area of time they take up at once is larger in materials with
higher difluctuation conductivity). Most intriguingly of all, when two singularity-sustained reality fluctuations,
which have very large fluctuation strengths since their temporal area and thus their chronovolume is so large, approach each other
and release diflux waves at a cosmic scale, these extremely powerful diflux waves have been "observed" to have patterns similar
to the wave patterns of conscious thought, and lifeforms that have spent extended areas of time near a reality fluctuation
and endured the spacial headache of doing so have reported that during their time near the reality fluctuation, they felt more intelligent
and able to think more at once, as if they were "more conscious" during their time near the fluctuation than at any other time.
It's been shown that the materials that lifeforms' brains are made of tend to have very high difluctuation conductivity,
and if SQRF theory is to believed, there might be diflucutation repulsion occuring between the particles that make up a lifeform's brain
thanks to the high difluctuation conductivity of neural materials, with the forces holding the particles together
(strong force, electric and magnetic forces, molecular magnetism, ezzolmisation in some cases, maybe even gravity, etc.)
ensuring that the particles remain closer than their difluctuation equilibrium distances so difluctuation repulsion can be sustained.
When all of these theories about diflux waves are put together, from their inability to actually affect the universe
(like how free will is an illusion) to their ties to the reality fluctuations that create them and their movement that isn't really movement
(like how consciousnesses appear to be tied to their bodies but do move through time) to their ability to exist in different states
at the same points in time (like a consciousness's thoughts and memories, the only other thing known to also be able to
have different states when returning to the same point in time) to the observation of possible conscious thought from diflux waves
during a singularity collision and the high difluctuation conductivity of neural materials... it seems like diflux waves
and consciousnesses are very, very similar. If these theories are to believed (one of the theories in this conglomeration
is that diflux waves exist at all, of course, as without such an assumption the rest of the theories are moot), then diflux waves
and consciousness are one and the same. Under this theory, which assumes SQRF theory to be true,
then a consciousness is actually the sum of the diflux waves created by the difluctuation repulsions between all the particles across its brain,
a conglomeration of diflux waves that has become large enough to be self-aware. With that, we've gained a way to measure consciousness:
if consciousnesses are combinations of diflux waves, then the square reliflux (rf2) can be used to measure consciousness.
 Chapter 8: Light and Energy
Chapter 8: Light and Energy
This chapter wasn't part of my original plan for extending my research of Lartravera beyond the base units, but as my
research continued, I realized that the previous chapters haven't told the whole story when it comes to energy in Lartravera... and since I
haven't mentioned the candela since Chapter 1, I might as well revisit photons and vision along the way.
Energy, Action, and Time
As mentioned back in Chapter 2, energy can be defined as matter multiplied by the square root of space of possibilities:
this could be measured in kg*m1.5/s, a unit called the Kristine. But what is energy, actually? In our world, energy is
defined as the ability to do work, which in turn is the action of exerting forces on the surrounding system. In other words, energy in our
world is the ability to cause changes to a system: the more energy a particular particle, object, etc. has, the more change to the system it's
in that it can cause, and causing these changes uses up this energy... or, more accurately, it transfers the energy to another part of the system,
often into a less usable form, such as turning kinetic (motion) energy into internal (heat) energy. However, there's a particular definition of
"change" in play here: in our world, forces cause acceleration, and a particle moving at a velocity in a vacuum (i.e. without forces like gravity
and friction affecting it) will remain at that velocity. A particle/object at a constant velocity has a constant amount of kinetic energy,
and as far as motion is concerned, it's only when acceleration gets involved that energy starts transferring and changing. This means that if
we define a change in position as a change (as opposed to only defining a change in velocity as a change and a change in position as merely
relative), then energy is actually a measure of change over time (transfers of energy are thus changes in change over time, which makes sense
because transfers of energy cause forces which cause acceleration and deceleration, i.e. changes in change in position over time)... and that's
the definition of energy I'm using to describe energy in Lartravera. Energy in Lartravera relates to all forms of change, which often involves
motion (such as velocity, though I should note that thanks to cosmic friction, even a particle moving in the vacuum of space requires a miniscule
amount of power to truly maintain a constant velocity; constant energy alone could only maintain a constant velocity if there were no quantum
reality fluctuations) but doesn't always (for example, temperature in Lartravera definitely involves energy since an atom with more internal
energy has a higher streggis, but since gress-waves aren't really waves (they're just a way to visualize an atomic process) it doesn't necessarily
involve motion. Distortions in spacetime caused by reality fluctuations can also relate to energy and power despite not requiring motion; more
on that in a moment). In our world, conservation of energy dictates that energy remains constant in a closed system; this is true in Lartravera too,
and there's an explanation as to why. I mentioned back in Chapter 6 that the spherical model of time assumes that the further from each other two
states of the universe are from each other, the further apart in time they are in time, but this is true in all models of Lartraveran time,
not just the spherical model, because this concept is how Lartraveran time is defined. Since different lifeforms perceive time at different rates,
and in Lartravera's case in different directions and pathways as well, Lartraveran civilizations needed a universal definition of what time is
that doesn't rely on the amount of time a single consciousness is experiencing at once. The most common definition that many of them
came up with is that time is the difference between states of the universe;
the more different two states of the universe are from each other, the farther apart those states are on the plane of time.
To measure the amount of change in a system, you use a unit of action, which is defined as energy multiplied by time
(an example of action is that if an object moving at a constant velocity has a given amount of energy, then if you multiply
that velocity by a certain amount of time, you get a certain change in distance. Therefore, if velocity multiplied by time measures change in
distance, then energy multiplied by time can be used as a measure of amount of change in general), so it's measured in J*s in our world, but it's
measured in Ki*s in Lartravera. A pair of points in time at a given interval of time away from each other will have the same difference in state
of the universe (or any other closed system, though of course no other such closed system exists as far as I know) away from each other as any
other pair of points at that same interval of time away from each other (by the definition of time), so a given interval of time will always
correspond to the same amount of change and thus the same amount of action. This means that the rate of action over time is constant by the
definition of time, and since energy is action/time, the total energy of the universe (or any other closed system) must be the same at all
points in time. Therefore, conservation of energy applies in Lartravera.
MDP Equivalence and Related Equivalences
However, just as conservation of energy has one notable exception in our world, it has a notable exception in Lartravera.
In our world, extremely powerful reactions such as nuclear fission and fusion violate conservation of mass and conservation of energy, as mass
and energy can be converted into each other in extreme circumstances. Conservation of matter is still an approximate law in Lartravera, and
so it follows that in Lartraveran physics, such an extreme reaction should convert matter (not mass, because mass is just an emergent property
and gressa does not have energy) into energy as well. However, matter cannot be converted into energy (or vice versa) directly: instead,
such a conversion must pass through a middle step, that being as a reality fluctuation. To explain this, we'll need to understand why natural
reality fluctuations expand and contract in a hyperspherical shape: when viewed via changes over time as opposed to static spacetime, a reality
fluctuation begins when a large amount of energy that previously manifested itself in space as quantum reality fluctuations (whenever energy
appears to completely disappear even when taking the internal changes of an object into account, such as via cosmic friction, that energy has
actually dissipated into space and is now generating quantum reality fluctuations) concentrates in a single distortion in space rather than
constantly creating new quantum distortions as usual, and this energy causes the reality fluctuation to expand. However, as the reality fluctuation
expands, the surface area of its border increases, thus the amount of quantum reality fluctuations that it experiences difluctuation repulsion
from also increases, and over time this interaction between the standard reality fluctuation and the quantum reality fluctuations forming near its
edge cause the reality fluctuation's energy to start being absorbed into the space around it, which causes the quantum reality fluctuations to
become stronger, and repeat, until eventually the quantum reality fluctuations have more energy than the standard reality fluctuation and the
standard reality fluctuation starts to collapse, with this process being accelerated as power returns from the reality fluctuation to the
surrounding space during the collapse. A stable reality fluctuation (such as a hypercylindrical reality fluctuation being caused by a singularity),
then, is a reality fluctuation with power equal to the energy drain being caused by the quantum reality fluctuations around it; and under
SQRF theory, all particles of matter are also stable reality fluctuations, thus a stable particle of matter has constant internal power equal to
the energy drain from the quantum reality fluctuations acting on it. These facts mean that the dissatus of a reality fluctuation
(measured in Dn = rf/s2; dissatus is a more useful measure than fluctuation strength when it comes to SQRFs because their temporal area
is so large and because the dissatus is part of what determines the type of particle they are), which is equivalent to matter under SQRF theory,
must also be equivalent to power. All of this means that the Lartraveran equivalent to mass-energy equivalence
equates three things rather than two: matter, power, and dissatus (if you're wondering how the dissatus of a reality fluctuation decreases as it
expands because the power is decreasing even though the fluctuation is getting larger and thus clearly increasing its dissatus, it's because most
of the distortion energy in an expanding reality fluctuation is contained within the barrier, and it's the barrier that loses energy to the
quantum reality fluctuations surrounding it, so while the dissatus of the interior of the fluctuation (which is the dissatus measurement that's
used when considering the spacetime density, distortion force, and volume of the reality fluctuation) is increasing, the dissatus of the barrier
is decreasing faster, so the total dissatus is decreasing), with the resulting laws of equivalence and conservation being referred to as
MDP equivalence. In particular, MDP equivalence means that matter can be converted into power in Lartravera rather than energy.
If we multiply all of these quantities by planar time, we get action from power and fluctuation strength from dissatus,
while the quantity we get from multiplying matter by planar time is a measurement of how much influence the existence of matter has on the
events of that area of time, a quantity known as lidaros (measured in kg*s2); this counterpart to MDP equivalence is called LRA
equivalence, though it's less useful than MDP equivalence. The equivalence between these two would be MDP equivalence multiplied by linear time
or LRA equivalence divided by linear time, which has energy as one piece, matter multiplied by its linear-time lifespan
(this quantity is known as temergotal, measured in kg*s) as the second piece, and one-path fluctuation strength
(the "fluctuation strength" of a reality fluctuation measured over a linear 1D path through time instead of its entire 2D time area,
measured in rf/s = Dn*s) as the third piece; this one is called TOE equivalence, and it's also less useful than MDP equivalence
(it's debatable which of LRA equivalence and TOE equivalence is more useful than the other).
Since particles of matter (SQRFs) have constant dissatus and thus constant power, conservation of energy combined with the fact that the energy
they're outputting is returning to space means that eventually they'll run out of energy to stabilize themselves with and the quantum reality
fluctuations will cause their collapse. This means that all particles of matter have finite lifespans, though in practice particles often live
much longer than their supposed lifespans by absorbing energy from the space around them. This means that if some of the power in matter is
converted into other more useful forms of power, the power that remains in the matter may not be enough to keep the matter from
decohering, so conversion of matter into power will only result in finite energy, but since it's still power being generated rather than energy
alone, a matter-to-power conversion done carefully is far more efficient at energy generation than even complete conversion of mass into energy
in our world. Though a single particle of matter has a very small volume, it's theorized that the spacetime density difference and thus the
distortion energy inside an SQRF is much higher than in a usual reality fluctuation (this extreme difference and thus extreme fluctuation border
strength is what allows an SQRF to act as a "solid" particle), so while the dissatus of a single particle of matter in SQRF theory is still small,
macroscopic amounts of matter are converted into very large amounts of dissatus when passing through a reality fluctuation barrier strong enough
to decohere the matter (similar to how a small amount of mass converts into a very large amount of energy in our world). Distorting spacetime
takes a lot of energy, and so reality fluctuations in general tend to have very high energy, which means a standard reality fluctuation has to
have a lot of power to outpace the quantum reality fluctuations eating away at it enough to reach macroscopic scales. These two facts combined
mean that matter contains a LOT of power, and when you combine this with the fact that what's being generated is power (albeit over a limited time)
rather than energy alone, it's clear that for a sufficiently advanced Lartraveran civilization, the amount of power and energy available is
practically limitless...
Photons
Since converting matter into dissatus most often happens when matter crosses a reality fluctuation barrier powerful enough to
decohere the matter entirely (which under SQRF theory means that the stable particle dissolves and the dissatus inside it becomes part of the
reality fluctuation that it was crossing), and all processes in Lartravera can be reversed, it's possible for even an otherwise sustained
reality fluctuation (one that's in equilibrium with the quantum reality fluctuations constantly forming and disappearing around it) to
slowly decay thanks to particles of matter being created on the edge and flying off into space, thus slowly taking away the dissatus of the
reality fluctuation in the Lartraveran equivalent to Hawking radiation... but how are dissatus and power converted into each other? When the
power contained in a reality fluctuation as dissatus is extracted, the reality fluctuation becomes weaker, and thus extracting the power from
a previously sustained reality fluctuation will cause the reality fluctuation to collapse, which once again means that this method of power
generation can only generate a finite amount of energy... which is inevitable, of course, because of conservation of energy. The most vast
source of energy in Lartravera is from space itself (this energy takes the form of the constantly appearing and disappearing quantum reality
fluctuations), but this energy is harder than almost any other form of energy to convert into other forms of energy, so civilizations that are
advanced enough to use macroscopic reality fluctuations but not advanced enough to use quantum reality fluctuations will have to use the
next-best options. In most natural circumstances, a reality fluctuation with more dissatus (which is equivalent to power) than the
dissatus (causing energy drain) of the quantum fluctuations around it will expand (which means some of this dissatus moves from the barrier
to the interior while some of it is lost from the barrier to the surrounding space), but sometimes a stable reality fluctuation won't do this:
instead, the excess dissatus will congregate at the barrier and then fly off as separate distortions in space. These distortions are the
Lartraveran equivalent of photons: they're carriers of energy. Photons in our world act like waves, but in Lartravera they're distortions in space.
Unlike reality fluctuations, photons don't have a barrier: their distortion in space is gradual, i.e. 0 df at the edge of the distortion,
a certain value at the center, and a gradual increase from 0 df to the central distortion force as you get closer to the center of the photon.
Assuming a spherical photon where the distortion force increases linearly as you get closer to the center of the photon (so if there's 5 df
of distortion force at the center of the photon, the distortion force is 2.5 df at any point in the photon halfway between the center and the
edge), doing some integration (I used WolframAlpha for this) reveals that the total dissatus (dissatus is the measure here since
Dn = df * m3) of such a photon is πr3f/2, where r is the radius of the photon and f is the distortion force at the
center of the photon. This kind of photon is called a line-sphere photon, and while it's the simplest shape of Lartraveran photon to understand,
there are many photons in Lartravera that have nonlinear increases in distortion force as you go closer to the center of the photon,
and some photons aren't even spherical! However, photons generally carry energy, not power, which means their dissatus will decrease over time
because dissatus is equivalent to power and the photon has a finite amount of energy to output before it runs out, and therefore a photon
in Lartravera (even one that doesn't hit any matter) has a finite lifespan before its energy is completely returned to space via
quantum reality fluctuations, and a photon loses energy due to cosmic friction over its lifespan. On the other hand, the fact that a
sustained reality fluctuation expels photons because of excess power (energy generation over time) but expelling a photon only transfers
energy means that a stable reality fluctuation that's expelling photons does so at a constant rate as long as the reality fluctuation
remains stable. Because photons don't have a fluctuation barrier, converting them into other forms of energy is easy: when a photon transfers
energy to matter, what happens is that the matter absorbs some of the spacetime distortion from the photon, and this distortion generally
becomes an increase in space of possibilities for the matter. If a photon collides with another photon, the two distortions in space
combine into a larger distortion, meaning that when two photons collide they merge into a larger photon. Though it's possible for a reality
fluctuation to expel a distortion in space that does have power, this distortion is no longer scientifically considered a photon, but rather
a stable reality fluctuation (it's stable because of the power) that happens to act like a photon. In our world, photons are the way that
energy from stars finds its way into other forms, and thus they're an abundant source of energy. Though the energy of space itself is
the single most abundant source of energy in Lartravera, photons (such as those from reality fluctuations) are still a good option for
civilizations that don't yet have the technology to extract energy from space itself, especially for a civilization advanced enough to
create their own photon-expelling reality fluctuations.
Lartraveran Photometry
If we're talking about photons anyways, I might as well explain some things about sight;
after all, the candela is an SI base unit, despite the fact that photometric units are defined around human eyesight and don't mean
anything as far as the laws of physics or even the principles of biology on Earth (different animals have different eyesight ranges, after all)
are concerned. Vision is a topic that varies heavily from species to species, and this is especially true when we're talking about a
whole universe with lifeforms very different from each other. Not all lifeforms have a sense of sight, and for those that do, not all of
them rely on photons for their vision. There are still many lifeforms in Lartravera that do see photons, but even considering just those
lifeforms, they all have many different ways of seeing things. The most common method of photon vision in Lartravera is the "dispectral" method
I mentioned back in Part 1, where a lifeform has two visual receptors, one of which sees light in one range of the spectrum and the other of
which sees light in another range of the spectrum, and the brightness the lifeform perceives coming from a single point of their vision is based
on the product of those two amounts of light because the two visual receptors rely on and amplify each other. Not only do these visual receptors
see different areas of the spectrum, but the light spectrum itself is far larger than it is in our world because it has an extra dimension.
In our world, the spectrum of light only has one dimension, the frequency of the light, but in Lartravera the spectrum of light can be defined
in several ways but has two dimensions in all definitions. The most common dimensions used to define the spectrum are the radius of the photon
and the photon's "gradient", i.e. how quickly the intensity of the light (which is actually the distortion force or the distortion energy
depending on the lifeform; the former case means that photons appear the same brightness to those lifeforms regardless of spacetime resistance,
while the latter case means that light appears less bright in areas of greater spacetime resistance since a spacetime distortion with the
same dissatus causes a smaller distortion in spacetime (less distortion energy) in areas of higher spacetime resistance) increases as you get
closer to the center of the photon, measured in df/m or dz/m. Other dimensions that I've seen used in diagrams of the spectrum of light
for different species in Lartravera include the photon's volume, the dissatus of the photon, the distortion force or distortion energy
at the center of the photon, the average distortion force or distortion energy of the photon, and even less intrinsic values like the
velocity of the photon or the distance the photon has traveled (and there are even more examples reserved for more exotic photons, but I'm
keeping things simple and focusing on line-sphere photons here). Though I have seen a few spectrum diagrams where the energy of the photon
is one of the dimensions, this definition is not as common as you'd think: (though it's certainly more common than the velocity and distance
examples): most lifeforms with photon vision don't see photons based on their energy, but rather based on more physical values related to
the distortion which the photon actually is (as while carrying energy is what defines a photon, said energy is contained in the form of
spacetime distortion until it's transferred). Though there are all sorts of definitions of the dimensions of the spectrum of light, with
different definitions working best for different lifeforms, we can generalize for some of the units as long as we stick to lifeforms with
dispectral photon vision. If the candela is a measurement of how visible light of a single visible point on the spectrum is and the
square candela is a measure of the actual perceived brightness from a point, then the unit of brightness from an entire light source would be
cd2*m2/m2 = lm*cd, not lm2. The square lumen would be a unit of radial brightness multiplied by
solid angle again, which isn't useful for measuring radial brightness but does have a rare use, as thanks to photon merging some kinds of
light sources actually do become more potent at generating visible light when they do so over a larger angle, so the square lumen would be useful
to measure the efficiency of that device. Since the candela is a measure of visible light emitted over time, the visibility of a single
photon or a set amount of photons is measured in cd*s in our world, while in Lartravera you'd measure the visibility of a given amount of
photons in cd2*s. Though the square candela and the radial brightness unit of lm*cd would work in linear time, it's important to
remember that lifeforms see a certain amount of planar time at once, so dividing photon visibility by planar time rather than linear time is
useful to measure the brightness that a lifeform is actually seeing if they're not focusing their vision on a particular point in time
(like how we can focus our eyes on a particular object or point in our vision; Lartraveran lifeforms can typically do that too, and they can
focus their vision both spacially and temporally), which would give units of cd2/s for planar time point brightness and lm*cd/s
for planar time radial brightness. Luminous efficacy (how visible a light source is compared to the power it's outputting, as a photon with
more energy isn't necessarily brighter for us; this increase in energy might move its frequency out of our visible range) is measured in
lm/W in our world, and in Lartravera it can be measured in lm*cd/P in linear time and lm*cd/P/s in planar time. Units for other photometric
quantities like illuminace (measured in lux = lumens/square meter) follow a similar principle, i.e. being the same as the unit in our world
except multiplied by a candela, and divided by a second as well when discussing planar time instead of linear time.
As I said previously, vision is a very subjective thing to come up with units of measurement for, so the
best way to understand Lartraveran photon vision is to give some examples rather than trying to explain general principles. The last time
I gave a lifeform-specific example when discussing Lartraveran physics was when explaining Skreeeeeeena's system of currency, but
Skreeeeeeena's people can't be used as an example for photon vision because Skreeeeeeena's people don't see photons, they see charges;
the people of Skreeeeeeena have two visual receptors, one of which sees pure positive littra charge as one primary color, pure positive
darra charge as one primary color, pure negative littra charge as a primary color opposite to the positive littra color (colors in their vision
can cancel out with each other, which is not how colors work for us), and pure negative darra charge as a primary color opposite to the
positive darra color, with other colors coming from mixes of littra charge and darra charge, and objects with more charge being brighter.
Skreeeeeeena's people still have a type of dispectral vision, but instead of two areas of the light spectrum, one visual receptor sees
particle charge as previously described, while the other visual receptor sees with the same system but it sees molecular charge instead
(and the four primary colors correspond to the four directions of molecular charge). Because nonzero charges are so much more common
in Lartravera than in our world while photons are rarer than in our world due to their finite lifespans, charge vision is actually more
common in Lartraveran lifeforms than photon vision is, and it's easier to describe than photon vision is since there's no complex 2D
spectrum of visible charge for most lifeforms that have charge vision, it's just "color is based on direction of the charge, brightness
is based on magnitude of the charge". Though the commonality of charge vision means that photon vision isn't that important to discuss on
the scale of life in Lartravera as a whole, I'll still give an example here, that being Orblifacto, a civilization that spans several planets
and contains several different species of intelligent life, all of which have photon vision of some kind. One such species has very
typical dispectral photon vision: its visual receptors can see photons with radii in a certain range (a photon with a radius too small is
just absorbed as energy before it can make it to the part of the visual receptor that actually sees it, while a photon with a radius too big
fails to be perceived as a single photon by the visual receptor and so it's broken apart by the collision with matter and also turned into
energy without being seen; the photon is, of course, still turned into energy thanks to the collision with matter even if the visual receptor
does see it) and gradients in a certain range (a photon with a gradient too small isn't detected by the visual receptor, while the equivalent
to the eyelid blocks photons with gradients too high because they'll damage the visual receptors), which means that on the 2D spectrum of light
with radius and gradient as dimensions, the area of the spectrum that one of this species' visual receptors can see is rectangular,
with its other visual receptor seeing a different rectangular area of the spectrum. Another species in Orblifacto has ranges for its visual
receptors that have a sort of short-term memory (it's not actual memory, of course, since it's "remembered" by the body and thus subject to
the laws of time that conscious memory is not) of the photons they absorb, so they don't care about the time it takes to completely see a
whole photon, only about the total dissatus of the photon. Another species has a sort of short-term imprint on their vision left behind
by any photon that hits, so their vision cares about the velocity of the photon (as a photon moving slower will be seen for longer but will
have less brightness thanks to the imprint fading away) and about the point in the photon of highest distortion force (which is the center for
line-sphere photons and for many other varieties of photon). Another species has visual receptors that are very sensitive to change, so they
can only see photons with a very low gradient but have a very large range of visible radii, but they also have a smaller range of visible
radii for higher gradients because a photon of higher gradient does more damage to their visual receptors if they're in contact with the
photon for longer, so the areas of the spectrum that are visible to their visual receptors are triangular. Then there's a species in Orblifacto
where their eyes are a little different between each individual, so while they all have similar areas of the spectrum that each of their
visual receptors can see, the shape of those areas differs for each individual: some are rectangular, some are triangular, some are elliptical,
some are in various polygons, some are even in noncontinuous shapes (a single visual receptor for those guys has multiple smaller ranges of the
spectrum it can see rather than one larger range). There's a species in Orblifacto which has visual receptors that work independently from
each other, so the regular candela, lumen, etc. can be used for their vision rather than the square candela. Finally, there's a species in
Orblifacto that has three visual receptors instead of two, and they all still rely on each other, so the units used to describe its vision are
related to cubic candelas. Orblifacto is a demonstration that even when only considering photon vision, there are still a lot of
different ways a lifeform in Lartravera can see differently from another... and that's just when limiting consideration to photon vision.
One of the most advanced groups in Lartravera I've seen is a group of scientific divisions of civilizations that work together as a team I call
the Optical Conglomerate, in which each civilization sees differently: a few of them see photons of different ranges, a couple of them see
charges in different ways, one of them sees velocity and acceleration, one of them sees only particle-electrically neutral substances
in one visual receptor and only molecular-electrically neutral substances (which is anything that's not ezzolmisated) in the other visual
receptor (though of course a substance can be both or neither), one of them sees littra in one receptor and darra in the other, one of them
sees temperature, one of them sees mass, one of them sees energy, one of them has more than two visual receptors and sees a different
type of particle in each receptor, and so on, and together the Optical Conglomerate when working together can see just about every property of
the universe between them. Imagining what these varied forms of vision look like even in the square spectrum area case, the most rudimentary
form of photon vision, is nearly impossible for us humans; how can we imagine seeing colors in a system with more than three primary colors?
At least with higher dimensions of space (such as imagining 5D spacetime) we can imagine how their cross-sections would interact with 3D,
but since colors are a part of vision itself it's pretty much impossible to imagine what vision in a 2D light spectrum would look like,
and even more impossible to imagine what all the different types of vision displayed by the Optical Conglomeration would look like.
Lartraveran vision is extremely diverse, so if we tried to cover every possible way that a Lartraveran lifeform can see, we'd never see the
end of it.
Terminal Velocity
In our world, photons in a vacuum always travel at a constant velocity, and said velocity is c, the highest possible speed
the laws of physics allow and a speed impossible to reach for any particle with mass and impossible to go below (in a vacuum, anyways)
for any particle without mass. However, this is not true in Lartravera: for one thing, photons do not travel at identical velocities.
The velocity of a photon is one form its energy takes (the other being the dissatus of the photon that lasts for a limited time), and so
a photon with more energy will travel at a greater speed; this is often true of matter in our universe, but in Lartravera it's true of both
matter and photons. Lartravera does not have a universal speed limit like our universe does, and thus the relativistic effects seen at
speeds near c in our universe do not apply to Lartravera, but there are still limits on how fast things can travel thanks to cosmic friction.
The faster an object, particle, photon, etc. is moving, the more quantum reality fluctuations it's colliding with, thus the more cosmic friction
it experiences, and therefore the more power it needs to be able to output to keep moving at that constant velocity. However, energy being
drained from an object into space results in the quantum reality fluctuation becoming more powerful in a positive feedback loop, and because
of this feedback loop, there is a limit to how fast an object can travel, a terminal velocity that the object would require infinite power
to maintain but finite power for any speed under the limit, similar to how reaching the speed of light in our world requires infinite energy
for anything with mass. Unlike the speed of light in our world, an object can reach and even exceed its terminal velocity when given energy
from an outside source (such as photons giving energy to matter; photons themselves can exceed their terminal velocity at the moment of their
creation since they're being given energy by the reality fluctuation border creating them) since it still only requires a finite amount of energy
to reach thanks to the lack of relativistic effects, but it's impossible for an object to indefinitely maintain a velocity equal to or above
terminal velocity because cosmic friction will always drain energy from the object at such a velocity faster than any power source can provide
additional energy to the object. The amount of time that an object can have a velocity above its terminal velocity before being brought back
below it is generally microscopic, but while "superterminal velocity lifespan" depends on the velocity, the type of object in question
(and, when considering macroscopic objects rather than particles or photons, various properties of the material and the molecules and particles
that comprise it), and other factors, the terminal velocity itself depends on only two factors: the strength of cosmic friction in the space
the object is travelling through (i.e. the average distortion force of the quantum reality fluctuations, measured in df but represented by χ)
and the surface area of the object (an object with more surface area experiences greater cosmic friction because it's in contact with more
quantum reality fluctuations over time). The equation used to calculate terminal velocity of an object given its surface area and the average
distortion force of the space it's travelling through is simply v = F/(a*χ), where v is velocity (in m/s), a is surface area (in m2),
χ is average distortion force of space (in df), and F is Finavelann's constant, a universal constant with units of
(m/s)/(m2*df) = (s*m*df)-1. This does mean that terminal velocity would not exist in an area of space with no quantum
reality fluctuations and hence no cosmic friction, but several other laws of Lartraveran physics would also break down in the absence of
quantum reality fluctuations, and so far no such area of space is known to be possible to exist. The fact that objects with a greater
surface area have a lower terminal velocity means that smaller photons travel faster than larger photons and that tiny particles can travel
across the cosmos many orders of magnitude faster than the spaceships of civilizations, but advanced civilizations have ways around the laws
of terminal velocity, such as using compression fluctuations to reduce the amount of space they have to travel through to reach their destination
or by harnessing energy from space itself to power a spaceship, which also reduces cosmic friction for the spaceship since taking energy from
an area of space means reducing the strength of the quantum reality fluctuations there.
Planar-Time Action and Power
If action is energy multiplied by linear time and power is energy divided by linear time, then what do you get when you
multiply or divide energy by planar time instead? Since linear-time action (measured in Ki*s) is a measure of amount of change,
planar-time action (measured in Ki*s2) could be used to measure the total amount of variance in a particular system across a
particular area of planar time. I previously mentioned that the amount of action across the entirety of Lartravera over is always the same
for a given interval of linear time, which means that in a sense action is equivalent to linear time, so planar-time action is equivalent to
planar time, and if a system of units were defined with the unit of action being the same unit as the unit of time, then energy would be
dimensionless, which makes sense since the total amount of energy in the universe is always the same as long as you're willing to count
matter-seconds (temergotal) and dissatus-seconds (one-path fluctuation strength) towards the count of energy. Since linear-time power
(measured in P = Ki/s) measures rate of transfer of energy, planar-time power (measured in Ki/s2 = P/s) can be used to measure the
how mobile the energy of a given system is over an area of planar time. Now that I've defined planar-time action,
you might be thinking that fluctuation strength should be equivalent to that rather than linear-time action, and thus
matter and dissatus should be equivalent to energy rather than power, but there are two reasons this isn't the case. The first is that rules
of velocity and photon generation make it clear that a stable reality fluctuation of a given dissatus generates energy equally through
any direction in time, so it's generating energy over linear time, thus dissatus is equal to power. The second is that when traveling across
time in a line that intersects a reality fluctuation for less time, the change in its dissatus, especially at the barrier, is more
drastic over time as it expands and collapses faster, so even though the spacial volume it reaches is less, the total amount of action
performed is still the same if you also consider the quantum reality fluctuations acting upon the reality fluctuation in question.
Lartraveran time is confusing to consider all the implications of, and I'm sure reality fluctuation strength being equivalent to
linear-time action rather than planar-time action despite being a quantity that depends on chronovolume and thus on planar time has a more
intuitive explanation for those that are familiar with Lartraveran time, but if those two explanations didn't satisfy you then I suppose
you'll just have to take my word for it that because dissatus is equivalent to linear-time power,
fluctuation strength is equivalent to linear-time action.
 Chapter 9: The Lartraveran Cosmos
Chapter 9: The Lartraveran Cosmos
For the past eight chapters, we've pieced together the laws of Lartraveran physics across scales from the macroscopic
(mechanical units, some electrical units, states of matter, standard reality fluctuations, and energy and MDP equivalence) to the molecular and
atomic (gressa theory, the Lartraveran periodic table, molecular charge, other electrical units, gress-waves and temperature, and photons) to
the subatomic (particle charge, proton fields, quantum reality fluctuations, and SQRF theory)... but what do all these laws result in in the
grand scheme of things? For the final part of my analysis of Lartravera, we're going to look at the cosmos and the celestial bodies that inhabit it,
and ultimately the universe of Lartravera itself. I claimed back in Chapter 1 that duality is the principle by which Lartravera operates, and nowhere
is this more applicable than on the cosmic scale...
Planets and Moons
I've mentioned planets a few times throughout this analysis, so it should be obvious that planets
do exist in Lartravera. Planets come in many, many forms, far too many to count, and a big reason for this variety is the fact there are so
many more possible molecules in Lartravera than there are in our world. The sheer number of possible substances, materials, etc. on the
macroscopic scale is many, many times larger in Lartravera than in our world, so it naturally follows that planets come in many more forms as
well. The most common type of planet is still gaseous planets made of L1D1 (diatomic element #1), but the most common type of solid planet is
actually crystalline. While element #1 is still the most common type of atom because it's the simplest to form, and element #2 is still the
second most common, the most common elements after the first two are elements with more symmetrical proton fields, especially powers of two,
as elements with more symmetrical proton fields are more tightly held together, thus they're easier to form and harder to alter via nuclear
fission or fusion. Of particular note is element #4; whereas elements #2, #8, #16, #32, #64, and #128 (It's still up for debate whether a
stable isotope of anything even close to #256 exists, which is why the Lartraveran periodic table typically stops at #128. Elements near #128
like #127, #126, and #129 have no stable isotopes and do not occur naturally, but #128 is so symmetrical that it does have stable, natural
isotopes) are all electrically positive, #4 is electrically neutral and is thus capable of forming molecules between just #4 and #1, whereas
any other power of two element requires a negatively charged element to form a molecule. The simplest molecule between these two elements,
L4D14 and L14D4 (which are the same molecule, just with the opposite matters), forms a crystalline structure, and since
this molecule is the second most common molecule in the Lartraveran cosmos (L1D1 is the most common, L4D4 is the third most common, and L2L3D2D3
is probably the fourth most common), many planets are made of it. Though gaseous planets and crystalline planets are the most common types of
planets, planets can be made of all sorts of other materials, from rocky planets to icy planets to slimy planets to liquid planets
(whether cool or molten) to stringy planets to grainy planets to metallic planets to all sorts of other materials we can't even imagine
because there's no molecules in our world similar to the Lartraveran molecules that make up those materials. Since Lartraveran lifeforms
generally have a far larger range of temperatures they can survive in than we do, you can't really define certain planets as habitable
and others as inhabitable; it all depends on the lifeform in question, and lifeforms can exist on almost any kind of planet.
Planets are typically held together by gravity, but sometimes ezzolmisation is involved as well. Planets generally have solid centers due
to the sheer amount of pressure in their centers, but the exterior of a planet can be made of solid, liquid (yes, planets with liquid exteriors
are not unheard of, and I'm talking about liquid exteriors that go quite deep into the planet, as opposed to the thin (relative to the size of
the planet) layer of water Earth has; some of these liquid planets don't even have atmospheres, unless you count the liquid itself
as an atmosphere), or gas. A planet with an exterior/atmosphere in permeate state is possible, but since gravity has almost no effect on matter
in permeate state since matter in permeate state has near-zero mass, a planet with a permeate atmosphere will quickly lose its atmosphere
to space... unless the planet and the atmosphere are ezzolmisated in a way that attracts them together (an atmosphere in pure permeate state
can't be ezzolmisated, so this requires the atmosphere to be partially gaseous and partially permeate). Particle electrostatic force is much
weaker than gravity on macroscopic and cosmic scales because it's a matter force, but molecular electrostatic force, the kind of force that
piecewise ezzolmisation allows for, is on the same level as a mass force, thus it is comparable to gravity and can hold celestial systems
together when gravity fails to do so. A planet with an atmosphere in partial permeate state would have basically no typical
atmospheric pressure, but the planet and the atmosphere would be very heavily charged, which can provide a pressure of its own as well as
the potential for all sorts of effects similar to lightning, so it's pretty clear that living on a planet with an ezzolmisated partial permeate
atmosphere would be very different than living on a planet with a gaseous, molecular-electrically-neutral atmosphere. Of course, this doesn't
mean that an ezzolmisated planet is necessarily more dangerous to live on, as Lartraveran lifeforms usually evolve with a much greater tolerance
for electric charge than we do thanks to the abundance of charged matter in Lartravera. Planets in particularly cold areas of the cosmos
can end up in nodolib state, where gravity once again fails to keep the planet together, but at this point the atoms and molecules have
so little movement that even without ezzolmisation (which requires movement to work), particle electrostatic forces can still keep the planet
together, even if only temporarily. I really can't describe every type of planet seen throughout Lartravera, as the possibilities for the
materials planets are made of are just too vast to enumerate.
Planets typically don't have moons in Lartravera, as gravity is strong enough that when an object
large enough to remain in a stable orbit around the planet and be considered a moon (as opposed to an asteroid on a collision course) enters
a planet's orbit, its gravity usually influences the planet enough for them to both orbit around each other, and thus binary planet systems are much
more common than planets with moons in Lartravera, especially when the planet has molecular charge in one direction and the entering object
has molecular charge in the other direction. Even if the planets are mostly molecular-electrically neutral, the fact that planets are moving
at such high velocities means that magnetism between the two planets if one has an excess of one matter and the other has an excess of the
other matter can also play a role in keeping the planets attracted and orbiting each other. Though gravity does allow for systems of more than
two planets to form, typically the electrostatic and magnetic forces that cause binary planet systems will prevent such ternary planet systems
by repelling the third entering planet. Binary planet systems are actually more common in Lartravera than lone planets, but lone planets
still exist. When a lone planet does have actual moons rather than a second planet (binary planet systems almost never have moons due to
the aforementioned electrostatic and magnetic repulsion, though a binary planet system with moons isn't completely unheard of), it's typically
many smaller moons rather than a few larger moons (as if the moons are too large, one of the moons becoming a binary planet is very likely).
The most likely type of lone planet to have moons is a planet with a bunch of piecewise ezzolmisated chunks, and in this case the planet's
surface often ends up in strips and bands, where the rings/circles on the planet's surface that the moons orbit end up with an excess of
one kind of matter or charge (such as littra or NE molecular charge) while the parts of the surface that moons do not cross over end up with
an opposite excess (such as darra or SW molecular charge). I imagine this as if the planet appears as a black sphere with many linear white
strips across it in all sorts of directions, and since this is a sphere the strips loop around and intersect in many places. Of course, this
is an approximation: while the strips probably would be visible on such a planet, the planet would probably be made of more than two materials,
so even from the perspective of a particular lifeform whose vision does make a clear distinction between these "lunar orbit strips" and the
non-strip parts, the strips would probably appear in several colors and the non-strip parts of the surface would probably appear in a different
set of several colors (such as the strips being in purples and pinks while the rest of the surface is in yellows and greens)...
but since vision is so subjective, we probably shouldn't try to analyze colors here.
Temporal Polarity
Gravitational attraction should work in Lartravera in theory, but there's a problem with that. If two objects are attracted
to each other via an attractive force like gravity, then when the same direction is viewed moving in the opposite direction of time,
the two objects are being pushed apart by a repulsive gravity! How can gravity be attractive in one direction of time and repulsive in another
if gressa has no properties other than mass (and thus no properties that can be negative)? The radial model of time gets around this issue
because there's a "valid" direction in time, away from the origin, and so in the radial model gravity is always attractive when the viewing
direction in time is away from the origin and inconsistencies only appear in "invalid" directions of time... but in most Lartraveran theories
of time, including the other two major models (snapshot and spherical), all directions through time are equally valid, so how do theories of time
other than the radial model explain this? The answer is something called "temporal polarity", a property of all forms of matter.
Each individual particle can have temporal polarity, but so can atoms as a whole, as can molecules, as can ezzolmisated pieces of an object,
as can whole objects, as can any other tier of thing that a force applies to as a whole rather than just applying to its parts, and the
temporal polarity of a larger thing (like an object or a molecule) does not have to be the same as the temporal polarity of the parts
that comprise it. Temporal polarity can be positive or negative. When there's a force between two particles or atoms or molecules
or ezzolmisated pieces or objects (and so on) and the force is attractive when both things have a positive temporal polarity,
the force will be repulsive when both things have a negative temporal polarity (and vice versa).
If one of the things has a positive temporal polarity and the other has a negative temporal polarity,
the force generally won't act at all, but there are all sorts of grey areas and special cases that I don't understand yet
where interactions between a positive temporal polarity and a negative temporal polarity do result in a force. If you look at a system
as it changes in one direction in time and then look at it in the opposite direction in time, every element of the system will have
the opposite temporal polarity in the second view as it did in the first view; if you look at it in a direction through time that's
perpendicular to the first view, approximately half of the temporal polarities will be reversed. Temporal polarity isn't an innate property
of a thing without time, temporal polarities are only defined with reference to a direction in time. If the radial model is true, then
all things have positive temporal polarity in directions in time directly away from the origin and all things have negative temporal polarity
in directions in time directly towards the origin, with all other directions in time having some things with positive temporal polarity
and some things having negative temporal polarity. Since different levels of a system can have a different temporal polarity,
some forces can be reversed while others aren't, for example, you could have a situation between two objects where the objects themselves
have negative temporal polarity (so gravity is repulsive, as gravity is a mass force so it applies to the objects themselves), the objects
contain ezzolmisated pieces in positive temporal polarity and the first object has opposite molecular charge to the second object
(so the molecular electrostatic force is attractive), the atoms inside the molecules are also of opposite charges but they have negative
temporal polarity (so the particle electrostatic force between the atoms is repulsive), and finally the individual nucleons have positive
temporal polarity (so the strong force is attractive, as is the particle electrostatic charge between the protons and the electrons).
The strange thing about temporal polarity is that forces aren't always symmetric across it: for example, the strong force
(which holds an atomic nucleus together under positive temporal polarity) is actually weaker under negative temporal polarity than under
positive temporal polarity, which means that the electrostatic force between the protons (which is attractive under negative temporal polarity)
can hold an atom together under negative temporal polarity instead, thus atoms generally stay held together under both temporal polarities.
An atom with particles of negative temporal polarity could theoretically contain both types of matter (the strong force would attract
opposite matter and electrostatic force still wouldn't do anything), but because of magnetism now being repulsive and the fact that this
only works in one temporal polarity, such atoms are never stable and fall apart quickly. Because of temporal polarity, binary planet systems
often have the same matter type or molecular charge on both planets (as opposed to the expected opposite matter type or charge) so that
they're always attracted in some way: gravity attracts them under positive temporal polarity, magnetism and/or electrostatic force
attracts them under negative temporal polarity. Once two planets are actually orbiting each other, of course, the orbital velocities
(which are obviously also reversed when viewing from the opposite direction in time) help keep the orbit stable in both temporal polarities.
There's one notable exception to temporal polarity: difluctuation repulsion. Though difluctuation repulsion can obviously look like
attraction when viewed in different directions in time, difluctuation repulsion doesn't work like other forces do, and I'd say the best way
to define it is to look at it from the perspective in time that the diflux waves it creates has (since diflux waves, if they exist,
likely have actual paths through time), and from the perspective of its diflux waves, difluctuation repulsion is always repulsive
as long as it's active.
Stezzors
What do planets orbit around in Lartravera beyond each other? Not only are there many more types of planets in Lartravera
than there are in our universe, there are also many more types of stars in Lartravera than in our universe. The most common type of star is
something I call a "stezzor", which is a sphere of ezzolmisated gas. Since ezzolmisation comes from fast-moving particles and energy is based
on space of possibilities, the molecules inside the stezzor have a lot of energy, but the extreme pressure inside the stezzor means they can't
just move around freely. A stezzor is usually made of a lot of ezzolmisated pieces with the same molecular charge, so the resulting repulsive
force increases the space of possibilities and thus the energy of the stezzor's molecules further. Molecular electrostatic force and gravity
are constantly at odds in a stezzor (including at negative temporal polarity, since gravity becomes repulsive and electrostatic force
becomes attractive), but electrostatic force has the slight advantage, so (in positive temporal polarity; unless temporal polarity is being
discussed, assume the direction in time I'm referring to places all parts of the system under positive temporal polarity) the stezzor slowly
ejects molecules and ezzolmisated pieces into space. If this stezzor has planets orbiting around it (and given that a stezzor has a lot of
molecular charge, attracting planets to orbit around it is easy, since both gravity and electrostatic charge can do so; gravity for any type
of matter, electrostatic charge for matter of the opposite molecular charge), some of those molecules and ezzolmisated pieces will hit the
planets, at which point their contact with the ground (especially if the planet is not itself ezzolmisated) may disezzolmisate the molecules,
and since ezzolmisation is a higher-energy state than non-molecular-charged matter, this releases energy and can thus be used as an equivalent
to solar power. Stezzors being the most common type of star in Lartravera is a big part of why charge vision is much more common in Lartraveran
lifeforms than photon vision, but stezzors can release photons too: when the ezzolmisation of some of the matter in a stezzor breaks down as
the matter is ejected, the loss of molecular charge can also cause release of energy, which can come in the form of photons being formed and
released from the stezzor along with the charged matter. Over a stezzor's lifespan, it loses both matter and energy, but it also expands as
its density decreases, and this expansion means that the matter inside the stezzor has a larger space of possibilities and thus more energy
(though this is balanced out by the electrostatic force being weaker at larger distances). As a stezzor expands and ejects matter and charge,
it becomes brighter for photon vision (as the matter it ejects disezzolmisates quicker and more photons are released) but dimmer for
charge vision. Eventually, a stezzor's density becomes low enough that it reaches a critical point where the molecules reach the limit of how
far away from each other they can remain ezzolmisated, and this is also the limit of how far the gress-wave interactions can reach.
Smaller stezzors remain at this limit (thanks to gressange holding the atoms together), continously ejecting matter at a slowing rate and
fading away until, after a timespan that's orders of magnitude longer than it took to reach the end of its growth, all of the matter in the
stezzor has returned to space and the stezzor is no more. However, larger stezzors have higher pressures and electrostatic forces in their
centers because their mass and molecular charges are quadratically higher than smaller stezzors, so by the time they reach their gaseous limit,
the ejection of matter is too fast for the gress-waves to hold them together, thus the stezzor near-instantly converts to permeate state,
with this total loss of molecular charge resulting in a huge release of energy along with the superheated permeate expanding off into space:
this is the stezzor equivalent of a supernova, though it's not quite as dangerous as a supernova in our world is since permeate doesn't have
much interaction with other matter due to its practical lack of mass or molecular charge (and the temperature of permeate doesn't mean much either,
as there's almost no gress-wave interactions to make it heat up other matter; there are still occasional collisons between molecules of the
permeate and other substances, but these are infrequent enough that even a superhot permeate would take a long time to heat anything).
Since Lartraveran time is valid in all directions, the end of a stezzor in one direction in time is its beginning in the opposite direction,
so it follows that stezzors are born in two ways: cosmic gas slowly absorbing charged matter and becoming ezzolmisated, or cosmic permeate
matter clumping together and reaching a critical point where it suddenly becomes an ezzolmisated gas, gaining mass and molecular charge at the
same time. In fact, a stezzor that's born one way will generally die in the other when viewed on a linear path through time:
a stezzor born by slow expansion will speed up its expansion over time and eventually explode into permeate, while a stezzor born by
contraction will lose matter slowly enough that once it stops contracting and starts expanding, it will expand slowly enough that it will
remain gaseous and fade away, and of course when viewed from the reverse direction in time, a stezzor's birth and death appear to swap:
since this is Lartraveran time we're talking about, a stezzor's "birth" and "death" are subjective (and since a stezzor doesn't have a
direction in time like a consciousness does, there's no single direction in time to define the birth and death), and unless a specific direction
in time is defined, all that can be said is that a stezzor starts existing and eventually it stops existing, with one of those being caused
by a slow change in matter and the other being caused by a gas/permeate transition.
Conservation of Molecular Charge?
The fact that ezzolmisated matter generally has high velocities isn't the only reason it's a higher-energy state
than non-molecular-charged matter. Particle charge is not a conserved quantity in Lartraveran physics; if SQRF theory is true,
then particle charge, like many other properties of matter, is a useful illusion created by the specific distribution of distortion energy
inside a particle of matter/an SQRF. Even if SQRF theory is false, it remains true that particle charge is not a conserved quantity in
Lartravera (for example, a matter-decohering reality fluctuation border can destroy electric charge), though it is mostly conserved in
most situations. It's molecular charge that might be conserved in Lartravera... but how is this possible if molecular charge is the product
of littra particle charge and darra particle charge? As it turns out, whereas mass only exists as an emergent property as the product of
littra matter and darra matter, molecular charge comes in multiple forms. Molecular bonds and ezzolmisation linking cause molecule charge
to be distributed as the products of proton charges and electron charges, but charged atoms in a non-molecular state can still have
molecular charge if energized and aligned in the right ways to avoid becoming molecules, with the net charges of littra and darra being
multiplied to calculate the molecular charge instead of multiplying the proton charges and the electron charges separately.
This means that in non-molecular matter, molecule charge is often much higher than in molecular matter (because if there's +2 C net littra
charge and +2 C net darra charge in a particular amount of matter, this matter will have the full 4 C2 NE of molecule charge
if it's non-molecular matter, but those molecular charges will be canceled out entirely in standard molecular matter or at least reduced if the
matter is piecewise ezzolmisated (though full ezzolmisation can result in an even greater molecule charge: if there's +5 C of both proton types
and -3 C of both electron types, the total molecule charge under full ezzolmisation is (5*5)-(3*3) = 16 C2 NE)), and it's also
possible for non-molecular matter to have molecule charge in the directions NW (net charges of positive littra and negative darra) and SE
(net charges of negative littra and positive darra) as well as the typical NE (positive net charges for both matters) and
SW (negative net charges for both matters), whereas ezzolmisated molecules can only have molecule charge in the directions NE and SW.
There are also exotic particles of matter that I call ⊥-protons and ⊥-electrons, which come in both types of matter and have opposite charges
to their standard counterparts (so ⊥-protons have negative charge and ⊥-electrons have positive charge, but they still act like protons
and electrons in atom formation when forming an atom with other ⊥-particles rather than acting like the other type). While ezzolmisated
molecules made of only exotic atoms containing only ⊥-particles can still only have molecular charge in the directions NE and SW,
molecules containing both regular atoms and ⊥-atoms can have molecular charge in any of the four directions. If molecular charge is
conserved (and different civilizations disagree on this), then what happens when ezzolmisated matter is disezzolmisated
(and thus molecule charge is lost)? The molecular charge is returned to space, where it gives quantum reality fluctuations charge.
The catch is that only the magnitude of molecular charge is conserved, its direction is free to change in such a transfer, and it
appears that molecule charge tends to exist in the NE and SW directions in matter, but it tends to exist in the NW and SE directions in
space itself. This means that most matter does not feel electrostatic force itself, but molecules formed using ⊥-particles can,
which may explain why ⊥-particles are much more unstable than normal particles and thus rarely seen naturally: the enormous amount of
electrostatic force they experience from space once they form molecules with normal matter is so powerful that it decoheres them
(if SQRF theory is true, it can also be assumed that the configuration of distortion energy inside an SQRF that acts as a ⊥-particle
isn't nearly as stable of a configuration as the configurations of standard particles). If conservation of molecular charge is true
and space does have molecular charge within its quantum reality fluctuations, this means the quantum reality fluctuations should repel
and attract each other based on their charges, and assuming space has molecular charges might be a way to explain some properties of
difluctuation repulsion... oh, and using the electrostatic force from space might be another way for an advanced civilization to
propel and power a spaceship. Again, much of this only applies if conservation of molecular charge is true,
and it's probably the least-supported Lartraveran physics theory I've detailed here yet, except perhaps for the spherical model of time.
Other Types of Stars
Stezzors aren't the only star-like object in Lartravera, though they are the most common.
Other examples include:
- Ecopollors: Clumps of molecular-electrically neutral (they're only necessarily neutral in molecular charge;
as I've mentioned a few times already, most matter in Lartravera is not particle charge neutral), extremely low density gas that collapse
over time. Thanks to the low density, the particles inside an ecopollor start with a very high space of possibilities and thus very high
amounts of energy, then as the star compresses the matter's space of possibilities decreases and the lost energy radiates away as photons.
Ecopollors are born when cosmic permeate without much electric charge condenses enough to become a gas but condenses very slowly,
and over their lifespan their compression speeds up until they become liquid, at which point their energy radiance dramatically drops
but they continue compressing until they become solid, and sometimes eventually nodolib. From the other way around in time, ecopollors
can be born when a cosmic clump of nodolib or solid is heated up by outside heat, slowly expanding and thus generating internal energy
(some of which radiates away) as it turns into a solid, then a liquid, then a gas, and finally fades away into cosmic permeate.
- Crilators: A sort of mixture of stezzors and ecopollors, the trick to these is that they're made of dialati gas. Crilators both compress
and lose charge over time, and additional energy is radiated away as the disezzolmisation also causes the shape of the dialati gas to
become more loose, as the rigid shape of dialati gas is also a higher-energy state than loose matter since it takes energy from ezzolmisation
to hold it in that shape. Because crilators release energy in several different ways at once, they have much higher power
(rate of energy generation) than other types of stars, but they have much shorter lifetimes. There are several ways a crilator can die
or otherwise stop being a crilator: it can disezzolmisate enough that its dialati status collapses, releasing a bunch of energy then
becoming a stezzor; it can condense until it becomes a solid (skipping the liquid phase because it's a dialati gas), at which point the
release of energy via deshaping stops and it becomes a (possibly dead, possibly starting expansion) ecopollor; it can expand and lose its
shape as it becomes cosmic permeate; and other methods. Crilators are some of the most powerful stars in Lartravera, but they're also some
of the shortest-lived, as existing as crilator is by nature a temporary state.
- Fuposors: Stars that are powered by nuclear fusion, which is how stars are powered in our world. Whereas nuclear fusion and fission
can convert matter directly into energy in our world, in Lartravera any matter lost during such a process is typically decohered back into
space, so the energy that a fuposor radiates typically comes in the form of particles (or sometimes photons) ejected during the fusion.
A fuposor generally fuses less symmetric atoms into more symmetric atoms, such as fusing element #3 and element #5 into element #8, and since
more symmetric atoms generally hold less electrons, the spare electrons (along with some photons that may have resulted from matter decoherence)
can be radiated away. Since nuclear fusion and fission are the same process in opposite directions in time, fuposors can also be fueled by
fission, with a less symmetric atom splitting into multiple more symmetric atoms (such as element #13 splitting into elements #8, #4, and #1),
which also allows electrons to radiate away. Though fuposors aren't great at energy generation as far as their planets are concerned,
they often have very long lifespans, sometimes with periods of dormancy where a fuposor reaches a state of mostly symmetric atoms and
then outside energy (such as from quantum reality fluctuations) causes a chain reaction that returns the fuposor to a less symmetric state
and starts the fusion and fission again.
- Retakerors: These are basically giant stable reality fluctuations that are kept stable by having a lot of matter contained inside them.
The energy released from these is photons in high amounts and sizes, especially as the matter inside slowly crosses the barrier and is
decohered, turning into excess dissatus that congregates at the retakeror's barrier and eventually turns into photons. As a retakeror loses its
matter, it starts to collapse as reality fluctuations typically do, though this process is slower for a retakeror than for an
empty reality fluctuation thanks to matter conversion continuing as the fluctuation shrinks.
Some retakerors leave no matter behind once they've finished collapsing because it was all decohered before and during the collapse,
while others do leave behind a clump of matter because at some point during the collapse the barrier became too weak to decohere matter,
at which point the collapse finishes much faster. A retakeror generally forms when a clump of matter gets so close together
that it overcomes difluctuation repulsion and some of the SQRFs start to fuse together, causing a
distortion in space that expands from there and engulfs the remaining matter.
- Petixors: These stars are very extreme, as they're powered by the fusion, fission, and transformation of particles of matter themselves.
A petixor is like a giant photon, a distortion in space that increases gradually towards its center, except it also has a lot of matter inside it.
At the center of the petixor, the distortion is so powerful that it distorts the matter inside, changing the properties of the particles
(which, under SQRF theory, means properties like distortion energy and chronovolume) and turning them into unstable exotic particles,
which often then decohere on their own into excess dissatus for the petixor. The petixor itself decays over time and only lasts as long
as it does because of the matter decoherence sustaining it, as it loses energy to cosmic friction while some of its energy leaves it as
smaller photons that break away from it. Some exotic particles will escape the petixor as well, making petixors the largest known source of
non-standard particles of both matters. Petixors are born and faded more gradually than retakerors, as petixors are generally formed when a
matter clump that would otherwise become a retakeror still comes close enough to activate difluctuation repulsion and distort spacetime
but not quite close enough to overcome difluctuation repulsion and merge into a reality fluctuation, and they simply fade back into
non-distorted space rather than collapsing.
...and many other cosmic objects that could arguably be considered types of stars. Considering all of these objects under the
category of "stars" is a bit misleading, as they radiate energy in very different ways, some are more likely to have planets than others,
and ultimately Lartraveran societies generally consider each of these to be a different (except, perhaps, for crilators, which are
sometimes just considered special forms of stezzors and/or ecopollors) class of cosmic object. Still, as far as understanding Lartravera
for those of us who live in our universe goes, all of these cosmic objects have some star-like properties, most importantly their ability
to provide energy to their planets (if they have any) and thus to civilizations.
Star Systems
Like with planets, some types of stars are much more commonly seen in binary systems than individually, especially stezzors,
and since stezzors are the most common type of star, most stars in Lartravera are found in binary systems. The reason for this in the case
of stezzors, of course, is that two stezzors will heavily attract each other via both gravity and molecular electrostatic force due to their
ezzolmisation (whether the two stezzors have opposite molecular charges or the same molecular charge depends on the temporal polarities
during the formation of the binary system). Binary stezzor systems are also the type of star system that's most likely to have orbiting planets,
and that's because planets are more likely to form within them: when two stezzors attract each other via charge rather than just mass,
some of the charged molecules that are ejected from one stezzor will end up attracted towards the other stezzor rather than flying off
into space, and this attraction applied from both stezzors towards each other can create a clump of matter between the two stezzors,
then this clump starts attracting more matter from the stezzors, and eventually it becomes large enough to start having an orbit around
the stezzors of its own, thus a planet is formed. This means that the planets of binary stezzor systems tend to be similar in composition
to the stezzors they orbit and to each other, though absorbing leftover matter from the cosmic gas/permeate the stezzors were born from may give
them some variance. Whereas the solar system of a stezzor or binary stezzor system is often changing thanks to the interactions of
ezzolmisated matter, ecopollors usually have much more static (i.e. the planets and their orbits are mostly stable, new planets aren't added,
and planets don't break apart from overwhelming forces) solar systems once the ecopollor has condensed enough, though in the early days of
an ecopollor when it's very low density some of the gas can break off and form planets or even smaller ecopollors. If these split clouds
of gas condense quickly, they become planets, but if they condense slowly enough they can become smaller ecopollors, which means an
ecopollor's solar system often consists of multiple smaller ecopollors orbiting a larger ecopollor, though the smaller ecopollors and
eventually the larger ecopollor will probably condense over time and turn into planets. Similarly, a planet in another solar system
can sometimes expand and become an ecopollor, and a former ecopollor that was once the star of a solar system can end up becoming
a planet in another solar system. Crilators generally radiate energy at too fast a rate (i.e. have too high power) to sustain a solar system.
When two ecopollors or crilators enter a binary system, the matter contained within the two stars can influence each other,
and if the ecopollors or crilators are moving fast enough, this can cause ezzolmisation (in the case of ecopollors) or loss of
dialati stability (in case of crilators), turning both of the stars into stezzors. Other stellar transformations are possible as well,
especially for ecopollors, such as outside energy causing a solid former ecopollor to become condensed enough that the atoms squeeze
together and begin fusion and the former ecopollor becomes a fuposor, an ecopollor becoming enveloped in a reality fluctuation
and becoming a retakeror, a fuposor's matter becoming so squeezed together that it distorts space and becomes a petixor,
a petixor's exotic particles experiencing electrostatic force from space itself to such a degree that the distortion collapses
and the petixor becomes a stezzor, ecopollor, or fuposor depending on the conditions of the matter inside, and so on.
Whereas stezzors are often found in binary systems, retakerors are usually solitary because of difluctuation repulsion,
and petixors are usually solitary because if they get close enough to each other they'll merge into a single, larger petixor.
When two fuposors end up in a binary system, the result can be one of the longest-lived energy sources in the Lartraveran cosmos,
as one fuposor will generate energy from fusion or fission while the other fuposor absorbs some of this energy in performing the reverse process,
serving as a catalyst to continue the first fuposor's activity after it would have otherwise petered out.
Then there are all the possible multi-star systems created with multiple star types, some of which form ternary or even more complicated
systems in conjuction, but there's too many possibilities to get into here.
Cosmic Temperature Zones
It's possible for planets to form into orbits without a star, with two or more planets drifting through the cosmos
all orbiting each other (or orbiting a particularly large planet, such as a former or could-be-eventually ecopollor) rather than a central
star of any type. You'd think that these systems wouldn't have much energy, but in fact intelligent lifeforms can form and even thrive
in these systems. Whereas outer space in our universe is almost entirely at temperatures near absolute zero, Lartraveran space has a
wide variety of temperatures thanks to the energy contained within quantum reality fluctuations. Though Lartraveran space doesn't have
weather patterns, it does have temperature patterns, with volumes of hot space followed by volumes of cold space followed by volumes
of hot space and so on, with sharp gradients in between. Smooth transitions between temperatures in space are rare; thanks to
difluctuation repulsion and how temperature works, it's much more common for a particular volume of space to have a consistent
macroscopic temperature with the transitions between these "cosmic temperature zones", i.e. the fronts of the cosmos,
being no more thick than a few petameters (A light-year in our world is around 9.4 petameters, but you can't use the term "light-year"
in reference to Lartravera since photons don't move at a constant speed) and sometimes so thin (on the scale of meters or even smaller)
that lifeforms can actually feel the transition as it passes if they're not within an insulating atmosphere (atmospheres of Lartraveran planets
not only keep heat in when the planet is in a colder region of space, they also serve to regulate temperature and prevent too much heat
from getting in when the planet is in a hotter region of space). It doesn't make literal sense to measure temperature of space
(i.e. temperature of quantum reality fluctuations) since temperature is defined as a property of gress-waves via the same-matter equivalent
of the gressa interaction, but in this case "temperature of space" basically just means the temperature that matter tends towards when in
that region of space. The cosmic temperature zones of Lartravera are always in motion, so the only way a starless planet can sustain
traditional life is if its own velocity or the velocity of its planetary system is keeping up with a cosmic temperature zone and
remaining within it... but given the multi-path nature of Lartraveran time, any planet is bound to stick to a single cosmic temperature zone
over at least one viewing path in time (even if that path isn't linear, which it usually isn't), and so life, even intelligent life,
can and has evolved on starless planets in Lartravera.
Other Cosmic Objects
What other things exist on the cosmic scale in Lartravera beyond planets (and other smaller planet-like objects,
such as moons and asteroids) and the various kinds of stars? Stars and planets arguably already classify most of the objects in the
universe because planets come in so many different forms (especially in Lartravera), as basically any semi-spherical clump of matter
can be called a planet if it orbits a type of star. Just about the only other objects in our universe that we know of that we consider
distinct from planets and stars are stellar remnants, like white dwarfs, neutron stars, and black holes... so what stellar remnants exist
in Lartravera? The most common type of stellar remnant is clouds of cosmic permate, otherwise known as "cosmic permeations",
massive clouds of permeate matter that, by the near-massless nature of permeate, have a near-zero density and are almost completely neutral
in molecule charge. Cosmic permeations are the Lartraveran equivalent of nebulae, as the permeate they consist of can eventually condense
into stars: stezzors if they condense at a moderate speed, ecopollors if they condense slowly, fuposors if they condense quickly,
and petixors if they condense near-instantly at such a speed that difluctuation repulsion kicks in at just the right strength as to not
tear the newly-formimg star apart while still preventing its collapse from continuing, forming a distortion in space in the process.
Cosmic permeate can also condense into planets, though there are other ways for planets to form as well, such as forming from a binary stezzor
system. The remnants of ecopollors, fuposors, and petixors are often planet-like clumps of solid matter, and indeed many of Lartravera's
planets are actually former ecopollors (and vice versa). These remnants can often transform into other things over cosmic timescales,
such as dissipating into cosmic permeate, dissipating into gas but then starting to condense again as an ecopollor
(or becoming ezzolmisated as a gas and becoming a stezzor), condensing enough to ignite fusion or fission as a fuposor,
and so on; the nature of Lartraveran time means that stellar remnants and soon-to-be stars are the same,
it just depends on the direction time is being viewed in relative to that object.
There are some rarer, more unique stellar remnants as well, one of which can be formed from crilators. Most crilators become stezzors
or ecopollors long before they stop radiating sufficient amounts of energy to be considered a star, but if a crilator retains its dialati status
at a high enough rigidity by the time it finishes condensing, it can end up as a "cosmic power crystal", a star-sized crystal that differs
from crystal planets in two ways: they typically have a polyhedral shape rather than a spheroid shape because their dialati status remained
until they stopped being a gas, and their potent ezzolmisation makes them a vast source of electric power and energy for advanced civilizations
lucky enough to find them. There are other theoretical types of stellar remnants, but most stellar remnants are clumps of matter that could be
considered planets of various types, so we'll move on from that. When it comes to special cosmic things that aren't planets, stars, or
stellar remnants... well, there aren't many of those, because those three categories cover just about every possible arrangement of matter
on the cosmic scale. One example of such a special case is a "binariply ring", but these don't really count as an individual thing
as they're systems of planets. Specifically, a binariply ring is a ring of evenly-spaced planets without a star, that all orbit around a
single point in space at an even distance, and the amount of planets in a binariply ring is always a power of two, as two-state forces like
electrostatic forces and magnetic forces work with temporal polarity in such a way that each planet is most attracted to the planet directly
across from it, then their next most powerful attractions are to the planets 90° away, then the next most powerful are to the planets 45°
and 135° away, and so on, dividing down by twos and resulting in a binary ring structure when combined with the velocities the planets
already have; binariply rings travel across the cosmos as a single system despite the lack of a star, at least until some cosmic disturbance
(like being attracted to a star) ruins the balance and the ring breaks down. There are also velladors, which are basically clumps of matter
moving so fast and with such large spaces of possibilities that they have so much energy that cosmic friction makes them radiate energy
to the point where they're sort of like stars. Velladors typically don't have a solar system because their movement is so extreme and erratic,
and they really shouldn't be considered stars because they don't really radiate energy like other stars do, they just lose so much of it to
cosmic friction that a non-negligible amount of energy flies off into the cosmos and can be absorbed by planets or other bodies, even though
most of the energy still ends up returning to space itself. When a vellador does have a solar system, it probably consists of planets and
other bodies that it's stolen from other orbits in high-speed flybys, and the planets orbiting it won't have their orbits last for long
before they're flung away once more. Velladors aren't considered stars by most civilizations, but there are many civilizations that do
consider them a type of star even though they don't really fit the characteristics of one once you look closer, like how us humans used to
think meteors were falling stars.
Then there are "cosmocean tubes", which may be the most interesting natural cosmic formation I've seen in Lartravera so far.
Cosmocean tubes only form under very particular circumstances, and they're incredibly rare, but in Lartraveran time all rare but possible things
almost surely exist somewhen, so here's how a cosmocean tube can form. The energy generation of a fuposor slows dramatically once it's fused
all of its matter into symmetric (powers of two) elements, and at that point fission can no longer generate energy. Such fuposors are
generally considered dead at that point, as stellar remnants or planets rather than fuposors, but if there's enough pressure fusion can
continue: after all, element #8 is more symmetric than element #4 even though both are fully symmetric, so when two atoms of element #4
fuse into element #8, there's still energy release, though not nearly as much as when elements like #3 and #5 fuse into #8. This means that
if a former fuposor (which can include planets; common crystal planets are good candidates for this because they're made of elements #4 and #1,
though they have to be at pressures much higher than it would take for a planet with non-symmetric atoms to become a fuposor) continues to
sit there without outside energy affecting its atoms enough to return them to less symmetric elements, they'll continue to fuse their atoms
into larger and larger powers of two over very, very long timescales. This process generally continues until element #64
(fusing two atoms of element #64 into element #128 would still generate energy, but the pressures required to overcome the proton fields
of an element as symmetric as #64 are so high that fuposors with enough pressure at their cores to do so usually overcome
difluctuation repulsion and turn into petixors or retakerors instead), at which point the clump of element #64 lies there nearly completely dormant
until some form of outside energy acts upon it. When outside energy does act upon it, many things can come from that... but in order to form
a cosmocean tube, the "outside energy" specifically has to be a cosmic power crystal crashing into the element #64 clump, and the power
crystal has to contain a sufficient amount of a negatively-charged atom (usually element #3 since it's the most common negatively-charged atom).
This can result in the element #64 atoms becoming part of the crystal as the heat from the impact turns it back into a gas, and if the gas
retains its dialati state (which depends on how the element #64 atoms are spread through the gas), then when it condenses again
(thanks to the heaviness of the element #64 and the strength of the molecular bonds formed between the element #64 and the element #3,
it will very likely eventually condense again), the element #64 will now be part of the power crystal. I call this a "postfuse power crystal",
and while these do have some interesting properties that normal cosmic power crystals don't have (for example, their high symmetry makes them
very good at conducting electricity in specific directions through the power crystal and very good at NOT conducting it in any other direction),
the next step is significantly more interesting: if the element #64 spreads out in a particular way as the collision gas recondenses,
it can start a chain reaction that causes the gas to change shape and spread out farther and farther, becoming very long in two spacial
dimensions and very thin in the third. When this gas condenses into a solid, it becomes a "cosmocean sheet", a sheet of matter
(it's almost always shaped like either a square or a circle, though advanced civilizations have created artificial cosmocean sheets with
other symmetric elements, and they've found that while all of them can form circular sheets, square sheets are exclusive to element #64;
element #32 makes triangular sheets and element #128 makes pentagonal sheets. This is because element #64 has a charge of +4,
element #32 has a charge of +3, and element #128 has a charge of +5. Element #16 would theoretically form a "cosmocean rod", which is thin in
TWO dimensions and very, very long in the remaining one, but I have not yet seen a civilization capable of inducing a cosmocean rod to form)
that can have a radius terameters across or even larger but a thickness of mere meters or even smaller. Cosmocean sheets are very interesting
on their own (for example, if intelligent life formed on one, they would genuinely live on a flat world with an edge), but there's still another
step: over time, a cosmocean sheet tends to break apart in its thin direction due to the particular way it had to be ezzolmisated to form,
and eventually it splits into two even thinner cosmocean sheets. These sheets will reach a certain distance from each other, and then the
ezzolmisation will start to flip thanks to their velocities and they'll start to attract each other back together. As the sheets are being
pulled together, matter breaks off from both of them as if to form a third sheet between them, and for some cosmocean sheets this is indeed
what happens: they break apart into more sheets faster and faster as they come back together until eventually they all collapse back into a
postfuse power crystal in a rectangular prism shape or a cylindrical shape. For some sheets, though, the final step occurs:
though the matter breaking off from the sheets starts out breaking off slowly and far apart from each other that it's in permeate state,
as the sheets grow closer together and the matter between grows more numerous, they can condense into gaseous state
and then into liquid state, and there's a particular molecule that can form between element #64 and #3
that remains in a liquid state at high enough pressures to reach a critical point, where the push from
the liquid between the sheets is strong enough to perfectly counterbalance the sheets' attraction at the middle (whereas with other molecules
that can form between cosmocean sheets, they'll become a solid before reaching this point and hence form a third sheet). On the edges, the
attraction continues, and the sheets start closing in on each other... but only in one of the remaining two spacial dimensions, as the liquid
starts leaking out in cosmic-scale waterfalls that end up concentrating on two of the square's sides or two of the circle's quarters, and in
the end the sheets only touch in one of the remaining two spacial dimensions, forming a cylindrical surface of solid matter with a
liquid interior, with an open top and bottom where the liquid leaks out like two cosmic waterfalls into space. THIS is a cosmocean tube,
and it's one of the rarest natural sights in all of Lartravera (out of those that I've documented, at least).
These generally don't last long enough for any sort of aquatic life to evolve inside them,
as eventually a cosmocean tube will lose enough liquid that the tube gets close enough together that the remaining liquid becomes
solid, leaving the structure as a cylindrical postfuse power crystal.
The Lartraveran cosmos is full of all sorts of interesting objects we could never hope to understand here in our universe
(and many that we could hope to understand), and the ones I've mentioned thus far are only a small taste of what's possible.
Distortion Dots
What about black holes? I mentioned singularities several times in Chapter 7, so surely black holes must exist in
Lartravera too? Well, singularities in the literal sense (a point of zero size, finite mass, and infinite density) don't really exist in
Lartravera: what I've been referring to as "singularities" are almost singularities, that being SQRFs with a much, much higher dissatus
than any standard particle of matter, so high that they distort the space around them as well. Technically all reality fluctuations
distort the space around them, but this distortion depends on the distortion force in the reality fluctuation, and while SQRFs are much
smaller than standard reality fluctuations, the distortion force inside an SQRF is far higher than in a standard reality fluctuation.
SQRFs (and thus matter particles since they're the same thing) in large enough amounts can cause non-negligible distortions in space,
as seen when cosmic-sized clumps of matter form retakerors and petixors. A "singularity", which I will now call a "distortion dot"
because it's a more accurate term, is this taken to the extreme, an SQRF that's orders of magnitude smaller than a standard particle of matter,
but its dissatus is on a similar level to or even higher than a matter particle, and thus the distortion force at each point inside the SQRF
is much higher, high enough to distort spacetime on macroscopic and cosmic scales. Distortion dots don't last as long as matter SQRFs do
because their distortion in space exerts much more power than their dissatus suggests and thus they run out of energy faster than matter does,
but they still last long enough to create temporarily stable reality fluctuations that can have very large chronovolumes.
Distortion dots usually don't form from most kinds of stars; retakerors and petixors are the only kinds of stars
that can become distortion dots under almost all circumstances, and some of them just turn into regular SQRFs, i.e. matter,
instead, or more likely their energy just returns to space. Distortion dots can form from sudden quantum appearances,
but this happens much less than it happens for particles of matter, which already isn't very common.
Distortion dots generally create reality fluctuations rather than black holes, partially due to the nature of spacetime
distortions and partially because gravity is a mass force. The more common Lartraveran equivalent to a black hole is a reality fluctuation
with a very powerful matter-decohering barrier; these reality fluctuations don't pull matter in like black holes do, but anything that does
cross the barrier is destroyed. That being said, if a reality fluctuation is being sustained by multiple distortion dots (being kept at a
probably subatomic-sized equilibrium distance by difluctuation repulsion), then it's possible for the distortion dots to have mass together,
which can be anywhere from a mass even smaller than a single gressa atom to a mass larger than stellar objects. When a multi-distortion-dot
fluctuation has a mass on the larger end, then it can start to act kind of like a black hole... but not quite. Light doesn't move at a
constant speed and Lartravera does not have a universal speed limit, so no "black hole" can exist that absolutely nothing can escape from,
though higher-end "gravitational fluctuations" can be powerful enough to suck up all but the smallest particles (since smaller things have a
higher terminal velocity than larger things based on surface area). The inside of a gravitational fluctuation can't quite act like a black hole,
but it can come pretty close: space can be distorted to the point that there's no way out for matter trapped inside when viewed on a given
time path, but since all time paths are equally valid, there's always a way out on some path through spacetime. Also, due to the nature of
Lartraveran time, gravitational fluctuations can be repulsive as well. Neither black holes or white holes truly exist in Lartravera,
but with reality fluctuations sustained by distortion dots, it's possible to create things that are nearly black holes and white holes
(which are one and the same depending on the path through time being viewed).
Dutagrexes
When I originally heard the phrase "duality is the principle by which the universe operates" in my studies of Lartravera,
I took this to be a true scientific belief, and though many civilizations do believe it in a semi-scientific way, it turns out there are all
sorts of things in Lartravera that don't really exhibit duality on a macroscopic scale (several of the cosmic objects I've mentioned thus far
haven't had much to do with duality, such as retakerors, petixors, and cosmic permeations), even if on the microscopic scale everything comes
from interactions between the two matters. As I've learned since, the idea that duality is the principle by which Lartravera entirely operates
is actually more like a religious belief than a scientific one: it makes sense to a certain extent and it explains a lot of things, but it's
built on shaky foundations and there's all sorts of things that prove it false if you're willing to actually accept them, right down to
something as fundamental as there being three spacial dimensions instead of two. That being said, there is one more big point in favor of
duality beyond the ones I've already given throughout this analysis thus far: it governs the cosmos of Lartravera at its largest scales.
Lartravera has many large star clusters, ranging from thousands of stars to millions of stars. Star clusters on their own aren't anything special,
but once enough stars are close enough together, their energy starts affecting the space around them in a particular way, creating a region of
space I call a dutagrex, the Lartraveran equivalent of a galaxy (though dutagrexes are on average significantly smaller than the galaxies of
our universe). The energized space in a dutagrex is most energetic at its edge, and for reasons that may be related to diflucation repulsion
or might be some Lartraveran equivalent to dark matter, the energized space of a dutagrex is generally repulsive. This means that stars that
approach the edge of the dutagrex they're in are pushed back inside, while stars that approach the edge of a dutagrex from the outside are
pushed away. Towards the center of the dutagrex, its force is negligible, so the inside of a dutagrex is basically just typical
star-populated space (this includes its center, whereas galactic centers in our world contain supermassive black holes). The force holding a
dutagrex together isn't that strong, so stars can still cross through their edges from time to time. The force from a dutagrex acts based on
the energy of the objects interacting with it, so fast-moving objects (which have a lot of energy) and stars (which radiate a lot of energy)
are much less likely to cross the edge of a dutagrex than a slower-moving, low-energy object like a crystal planet. A dutagrex as a whole has
a two-state quality that I call its dutagrex state: it's either in "white state" or in "black state". These states, which are based on confusing
specifics of the energy of space, don't mean anything as far as the dutagrex itself is concerned, but they do mean something when it comes
to interactions between dutagrexes. Similarly to electrostatic force, dutagrexes have a force on each other (this force applies to the dutagrex
as a whole, not to the individual stars or other objects within it, but it does influence the stars within it by way of influencing the
dutagrex collectively) which I call grey-grex force, where dutagrexes of the same state repel each other and dutagrexes of the opposite state
attract each other (under positive temporal polarity, anyways; a dutagrex as a whole has a temporal polarity, which is mostly independent from
the temporal polarities of the stars and other cosmic objects inside the dutagrex). However, the energy from a dutagrex barrier also acts
upon other dutagrexes, which results in two dutagrexes of opposite states orbiting each other as a pair at an equilibrium distance. The
energized space between the two dutagrexes results in larger dutagrex edge forming around the two of them: a bidutagrex. A bidutagrex's barrier
is much weaker than a regular dutagrex, weak enough that it doesn't really have any effect on individual stars at all, but it also comes in
white state or black state. Individual dutagrexes mostly only feel the grey-grex force from their partner, but bidutagrexes of opposite state
attract each other via grey-grex force and repel each other with their edges as well (bidutagrexes can act on individual dutagrexes, but
usually don't because the dutagrexes are acted upon much more by their partner dutagrex than by the bidutagrex they create, as the radius of a
bidutagrex is significantly larger than the radius of the orbit between the partner dutagrexes that create it). The interaction between two
bidutagrexes creates an even fainter dutagrex edge (a tetradutagrex), then those also have pairs and create an even fainter dutagrex edge
(an octodutagrex), and so on, with pairs of pairs of pairs of pairs from individual dutagrexes up until the largest structures in all of
Lartravera (the increasing faintness of the edges for higher tiers of multidutagrex is balanced out by the fact they're acting on larger and
larger multidutagrexes which feel the grey-grex force and dutagrex barrier force more strongly). Not every dutagrex is part of these
binary chains, of course: there are some dutagrexes that don't have a partner, some that do have a partner but whose resulting bidutagrex
doesn't have a partner, and so on, and of course there are also some stars and planets and other celestial bodies that aren't
in dutagrexes at all. That being said, the structure of the Lartraveran cosmos at its largest scale is embedded in duality,
with dutagrexes orbiting in pairs, then the pairs orbiting in pairs, then those pairs orbiting in pairs, and so on,
potentially ad infinitum depending on whether Lartraveran space is finite or infinite.
Life and Advanced Civilizations
On the cosmic scale, life in Lartravera is not uncommon, and it has evolved in many, many forms across the cosmos.
If the theory proclaimed at the end of Chapter 7 is true, this is because consciousness is made of diflux waves, and difluctuation repulsion
is fairly common on the subatomic scale because every particle of matter is an SQRF. There are so many forms of Lartraveran life that I
can't do them justice with any amount of description here. Instead of trying to be even close to comprehensive, I'm going to just list
a bunch of notable facts about life in Lartravera, whether they apply to life as a whole or to just the kinds of advanced civilizations
that are actually visible on the cosmic scale. Though life comes in a vast array of shapes and sizes in Lartravera, almost all lifeforms
have solid bodies, as brains of other states of matter generally wouldn't be bound close enough together for diflux waves to propagate
through them and become conscious. Since a consciousness that consists of more diflux waves is more conscious and generally more intelligent,
the few lifeforms of other states of matter that do exist (and no, a lifeform with a liquid body but a solid brain doesn't count for this)
are generally not intelligent lifeforms, though I have seen a species known as the stequegeo that are made entirely of dialati gas,
with the brain being held together by dialati gas's property of retaining its shape. The most important difference between life in our
universe and Lartravera is the paths through time that consciousnesses take... but I've already covered that in great detail in Chapters 1 and 6,
so I won't go into that here (Other interesing things I've also already covered about lifeforms and civilizations include their uses for
reality fluctuations in Chapter 7 and the fact that different lifeforms can have vision that sees completely different properties of the universe
from each other in Chapter 8). When it comes to sources of power and energy, advanced Lartraveran civilizations have many, many options
(some of which are more efficient than others): electricity of particle charge and of molecular charge, draining the space of possibilities
from matter via compression, fusion and fission of atoms into more symmetrical elements, use of cosmic power crystals as massive
electric circuits, converting matter into dissatus via decoherement in reality fluctuations and converting dissatus into power by
reverse cosmic friction, using the temperature of space as a source of energy, harnessing the energy from space itself via
quantum reality fluctuations, and many, many more. Though cosmocean tubes are more well-known as cosmic tourist attractions,
I've also heard of advanced civilizations using them as cosmic aquariums or even as land to live on: since the surface of cosmocean tube
is so thin, there's a very high amount of surface area compared to the matter used to make them (though thanks to the thinness of the ground
and the fact that cosmocean tube surfaces are generally made only out of molecules of element #64 and element #3, the land can't be used for
agriculture or natural resources or anything like that; it's useful to build on, but to live on it there has to be constant shipments of
outside resources). Though Lartravera does not have a fundamental speed limit, the terminal velocities imposed by cosmic friction still put
a limit on how fast an advanced civilization's spaceships can travel. There are ways around this limit: I've already mentioned using compression
fluctuation highways to reduce the amount of space traveled through to reach the destination, but it's also possible to induce an
expansion fluctuation to surround the spaceship like a bubble, so it will be the expansion fluctuation that experiences cosmic friction
instead of the spaceship, and since the expansion fluctuation is larger on the inside than on the outside, its surface area will be
smaller than the spaceship's surface area inside it, therefore its terminal velocity is higher and it can travel faster
(as for the spaceship inside the expansion fluctuation, it still experiences some cosmic friction, but it experiences much less of it;
the distortion force of quantum reality fluctuations is much smaller inside a larger reality fluctuation than in non-distorted space because
most of the dissatus of space that would otherwise be forming quantum reality fluctuations is part of the macroscopic reality fluctuation instead).
The problem with these methods is that they can only be used on unmanned spaceships such as robot-operated cargo transport: consciousnesses
can't cross reality fluctuation borders, so any method involving entering a reality fluctuation won't work for a manned spaceship
(the bodies of lifeforms can be transported, but the consciousnesses themselves will be expulsed from their bodies). This is completely true
for compression fluctuation highways (as far as I know), but there actually is a way to use the expansion bubble method on a manned spaceship.
Since consciousnesses are unable to enter reality fluctuations specifically because of the difluctuation repulsion from their barriers,
a consciousness can enter a distortion in space that doesn't have a barrier strong enough to activate difluctuation repulsion (such as a petixor).
Thus, if an advanced civilization builds a spaceship with the capability to create such an expansion bubble, it can first create an expansion
distortion in space without a fluctuation barrier (like a giant photon/smaller petixor), then once all the passengers are on the spaceship,
it can redistribute the distortion energy in this distortion to create a barrier, thus creating an expansion fluctuation with the
consciousnesses already inside it. Of course, now the consciousnesses can't leave the fluctuation (or see outside it, so the ship's
navigational systems have to be able to show a screen of what's outside the fluctuation because the windows can't show that),
so the fluctuation has to be decomposed back into a barrierless distortion once the ship arrives at its destination, but the point is that
using an expansion fluctuation to increase a spaceship's terminal velocity is possible to do even on spaceships that are transporting lifeforms.
While we're on the topic of consciousness and reality fluctuations again, let's answer this question: what's the most
intelligent natural species in Lartravera? This may be surprising, but there actually is a single answer. Certain retakerors
have their matter squeezed close enough together that massive amounts of difluctuation repulsion happen between all of the matter inside them,
resulting in a concentration of diflux waves larger than any other species of lifeform (except perhaps for some of the cosmic-scale computers
with artificial consciousnesses that Lartravera's most advanced civilizations have created). These retakerors are known as "thinking stars",
and they're so intelligent that they're able to distort space, create matter, and basically exert godlike powers as they please inside them,
like sentient pocket dimensions that have complete control over themselves. The catch is that since consciousnesses can't cross
fluctuation barriers and the diflux waves between the matter inside a thinking star's body form inside the retakeror (since the retakeror
is the thinking star's body), a thinking star has no way to perceive anything outside itself, and so thinking stars are godlike beings
inside themselves that from the outside appear like a completely normal non-conscious retakeror, except perhaps for changes in its rate
of energy radiation and lifespan thanks to what the thinking star is doing on the inside.
Fate of the Cosmos
What is the ultimate fate of the Lartraveran cosmos? The most likely fate of our universe appears to
be slowly cooling and becoming less and less eventful until eventually nothing is left but subatomic particles floating through the void,
but what about Lartravera? Well, the entire concept of a final fate for Lartravera is a moot point, because the nature of Lartraveran time
means that if the universe had a so-called "final fate" then from a reverse direction in time this would actually be its beginning state,
and there's always a path in time that would take you to some other more interesting state. This is especially true in the spherical model,
where by definition every possible state of space is a single point in time and the entire sphere encompasses all possible states,
but it applies to the snapshot model too since all paths through time are valid in both. This leaves the radial model as the only model in
which the idea of an ultimate fate makes sense, since the radial model does have "correct" paths in time, all of which lead away from the origin,
thus we can suppose that all of these correct paths in time in the radial model eventually lead towards the fate of the cosmos, which means
that all points in time beyond a certain (very large) distance from the origin will have reached this fate. The fate of the cosmos is
inextricably linked with the rate of its expansion, and each model of time has a different belief about the expansion of space. In the spherical
model, space is defined as having a single, finite size, so reality fluctuations notwithstanding there is no expansion or contraction of the
cosmos as a whole. In the snapshot model, expansion and contraction of space both happen, and since all paths through time are valid it cannot
be said that the cosmos is specifically expanding or specifically contracting: it does both, depending on the path through time being viewed.
The radial model, on the other hand, supposes that the universe started from a single point in space at the origin of time, and that the universe
is always expanding when viewed on a linear path through time moving directly away from the origin. Thanks to conservation of energy,
all particles of matter as SQRFs have a finite lifetime, as eventually they'll run low enough on energy thanks to cosmic friction that they
can't output enough power to remain stable against said cosmic friction, so in the distant future in the radial model, all matter will have
eventually decohered back into energy for space if SQRF theory is true. Though quantum reality fluctuations can turn into new matter particles,
there will generally be a lot less matter in this distant future than there is in the frames of Lartraveran time that I've researched
(i.e. the areas of Lartraveran time that life exists and the cosmos is at its most interesting)... but even this will run out eventually.
In this theory of the fate of the Lartraveran cosmos, it's believed that the universe started (at the origin of radial time) not as a single point
but at a particular natural size where the energy of quantum reality fluctuations was at its maximum, and the expansion of space has actually
been the dissatus of space slowly turning from quantum reality fluctuations into distortion that's expanding space, and over time the energy of
space (in the form of quantum reality fluctuations) will go down as its dissatus (which in this case translates to its size) goes up,
and in the end the cosmos will reach its final size where all of the energy in the entire universe is dissatus in the form of expanded space,
at which point there's no more quantum reality fluctuations and no more matter, just completely uniform space at its maximum size. You'd think
that this process would slow down over time as there's less energy left for the expansion, but since Lartraveran time is defined by rate of
change in the state of the cosmos, once the matter is mostly gone and all that's left is the slow process of quantum reality fluctuation energy
depleting as it's converted into expansion of space, this process actually happens at the same rate for the remainder of time because it's
the only change that's still happening. Once the Lartraveran cosmos reaches this final uniform state, there is no more change that can happen,
which means that this state is the end of time: if a Lartraveran consciousness (such as a ghost, if those exist) somehow viewed this happening
from outside of the universe, its perspective in time would have to reverse direction once it hit this final state because there are no points
in time after that. This means that whereas the spherical model assumes time is a 2D looping surface of a sphere and the snapshot model
assumes time is an infinite 2D Euclidean plane, the radial model under this theory actually assumes time is a finite 2D hyperbolic plane with a
very distant edge, as opposed to an infinite 2D hyperbolic plane as previously thought...
...but don't worry yourself about this fate of the Lartraveran cosmos. This fate will only come
to pass if several theories about Lartravera are all true, and while SQRF theory is pretty likely to be true from what I can tell, which
model of time is true is much less agreed-upon, and the same goes for the expansion and/or contraction and/or other variance of the size
of the universe. It's much more likely that Lartraveran spacetime doesn't have a defined end or final fate... and even if it does,
an advanced civilization can always make sure its paths through time stay away from the end. There's a lot of possibilities when it comes
to the fate of the Lartraveran cosmos, and indeed the entirety of the Lartraveran cosmos has a practically uncountable number of possibilities.
In just about every paragraph of this part, I've only scratched the surface of what's possible and what exists in the Lartraveran cosmos,
and it's likely that in a far enough away area of time, all of the objects in the cosmos are very different and yet just as interesting as
the ones I've seen. Especially in the spherical model, but probably in the other two as well, if you can think of an object that could
conceivably exist given the laws of Lartravera's particles and molecules, it probably exists, thanks to the endless possibilities of time,
somewhere and somewhen in the Lartraveran cosmos.
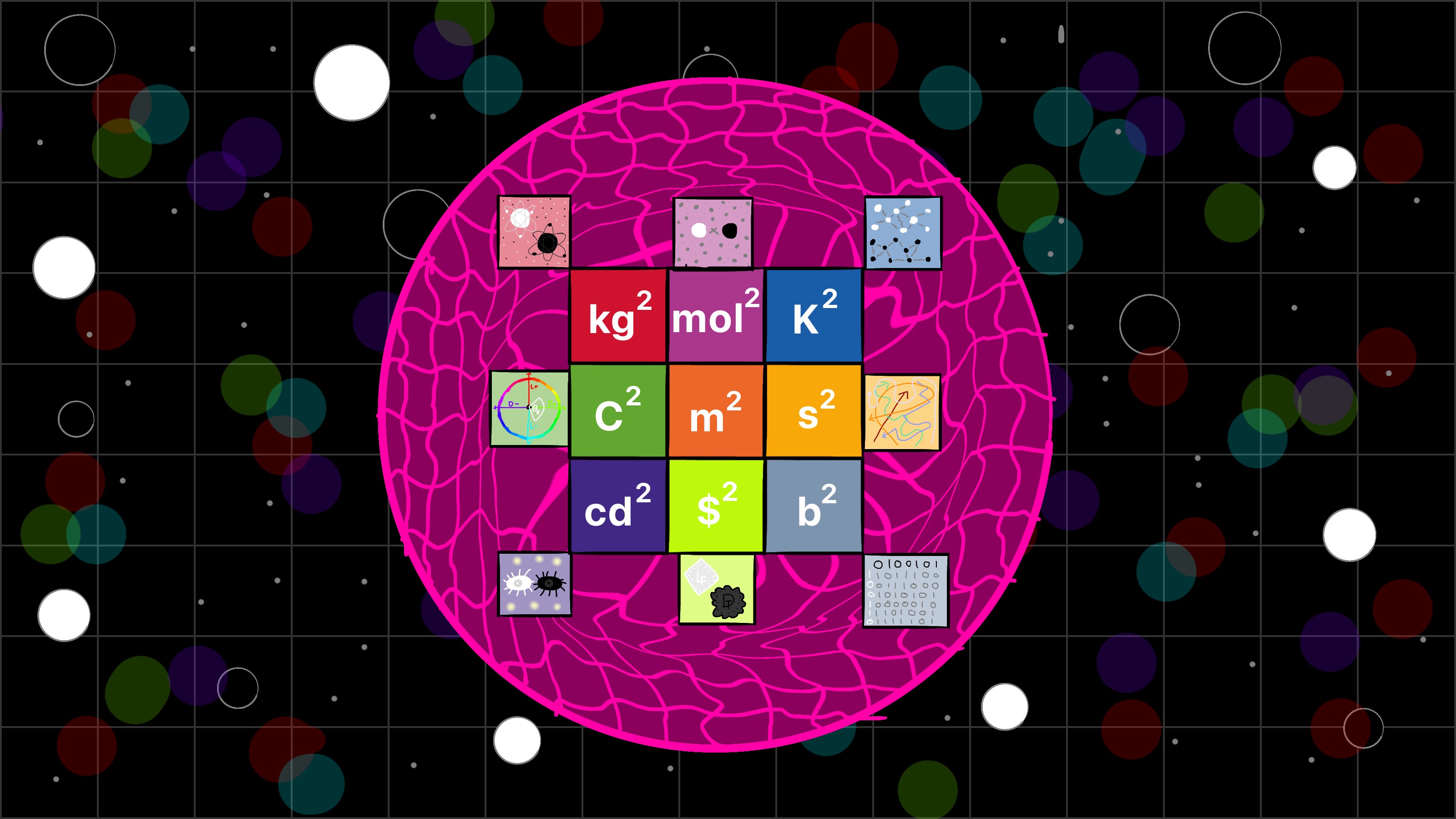 Conclusion
Conclusion
In our world, the absolute fundamentals of reality are, as far as we know, defined by the Standard Model of physics,
which defines the fundamental particles that comprise the universe and how they interact (though the Standard Model is incomplete; for one thing,
it has no explanation for gravity). In Lartravera, the fundamentals are
time having two dimensions instead of one
but space still having three dimensions,
the existence of reality fluctuations (distortions in spacetime)
and the fact that space is filled with constantly appearing and disappearing quantum-scale
reality fluctuations,
quantum reality fluctuations of specific types being able to stabilize and act as matter
(if SQRF theory is false, several more fundamentals need to be added to this list that are explainable by SQRF theory if it's true),
and time's definition as the rate of change of the universe. Everything else I've said
about Lartravera can be traced back to these fundamentals and the interactions between them. The particular configurations of quantum reality
fluctuations that can become SQRFs and the interactions between them lead to every property of matter, most importantly
the fact that the two types of matter work together in harmony instead of annihilating each other
as they do in our world,
as well as electric charge being two-dimensional. The interactions between littra and darra
lead to
mass being an emergent property of the two
that can be explained by the theory that there's a third, less "real" type of matter created
between pairs of one littra atom and one darra atom, and the interaction that creates this third type of "matter"
between the two different matters
may also be responsible for temperature when it occurs between two atoms of the same matter,
which in turn plays a major role in defining
states of matter on a macroscopic scale.
Reality fluctuations repel one another at close enough distances,
and difluctuation repulsion theoretically generates "waves" that experience a non-zero
area of time at once and can become self-aware when enough are put together but have no impact on the rest of the universe.
The behaviors of diflux waves, in turn, define consciousness and all of its weird properties,
such as its paths through time and the ability to retain memory independently of the passage of time,
but since time defines change, the plane of time itself has nothing to change over and is thus unchanging,
so there is no free will.
The behavior of the gressa interaction, when combined with the behavior of planar time,
allows additional bits of information known as grey bits to be stored and manipulated
despite not really being given,
but to do so the device storing the grey bits must have a consciousness so it can have
memory dependent on its own perspective rather than on the true passage of time.
The nature of space and time means that objects can exist in multiple points in space
over multiple points in time with different ratios between the two at different times, and changes in this "space of possibilities"
are what forces cause.
Space of possibilities is closely linked to energy, and since energy is
defined as change over time and time itself is defined by change, the amount of energy in the universe must be constant over
all intervals of time. The nature of time means that all processes are reversible, which leads to
forces causing reversed effects based on the direction time is being viewed in.
Quantum reality fluctuations cause cosmic friction, cosmic friction is responsible
for the collapse of reality fluctuations, the finite lifespan of particles of matter, and
the existence of a cosmic terminal velocity, and its existence proves that stable reality
fluctuations must be outputting power to stay stable,
which demonstrates MDP equivalence, which itself leads to LRA equivalence
and TOE equivalence. Reality fluctuations can
turn matter into dissatus and vice versa, and
dissatus and power can be converted into each other via cosmic friction.
Reality fluctuations with excess power can
eject temporary distortions in space without barriers,
which some lifeforms see as photons.
The energy contained within space via quantum reality fluctuations is responsible for
space having varying temperatures.
The behaviors of SQRF interactions like the interactions between charges,
the symmetries of proton fields,
the magnetic attraction that moving particles of opposite matters experience, and
the ability of electron fields to fuse together lead to the formation and properties of
atoms,
molecules, and molecular charge. Though molecules usually don't have any molecular charge,
some combinations of them can be molecularly charged via a motion-based process
called ezzolmisation, which has all sorts of uses, from
electric currents to
creating special states of matter to
powering stezzors to
holding planetary systems
and solar systems together.
At the largest scales of space, the energy of quantum reality fluctuations results in
repulsive borders of space that form giant, mostly self-contained volumes of space ("dutagrexes"),
which orbit each other in pairs of pairs of pairs of pairs and beyond. Beyond all that, the other things I've discussed (such as
advanced Lartraveran civilizations,
how society and culture and currency adapt to two-dimensional time, and
many of the objects seen in the cosmos) aren't really properties of the universe
but rather the things that have emerged from those properties. When it comes to what emerges from these properties, the possibilities are nearly
limitless... as beyond all else, the nature of time ensures that almost every possibility that can come to pass under the laws of Lartraveran physics
will come to pass at some point in space and time.
My analysis of Lartravera has covered a lot of topics, from
the basics of the universe and how squared versions
of the SI base units can be used to in measuring it to
the equivalents of kinematic units to
the ways atoms and molecules form and behave to
the principles and units of molecular charge electric circuits to
the definition and of temperature and the effects temperature has to
the possible natures of consciousness and time to
the definitions and rules of reality fluctuations and what their
existence means for the universe to
the definitions of energy and the behaviors of photons to
what all those things result in on the cosmic scale.
Our current understanding of our universe and the laws of physics that define it is still incomplete, and the same is definitely true of not
only my understanding of Lartravera, but also of the understanding of Lartravera that even its advanced civilizations have. After all, my analysis
used several theories that haven't been completely proven: gressa theory, the three theories of time (especially the snapshot model), SQRF theory,
diflux waves, and more (though these were the main theories I actually ran with; others were mentioned, but only the theories listed here were
really assumed to be true or at least played around with as if they were true afterwards, whereas the rest (like Delisha's Hypothesis) were simply
discussed then moved on from). Some of these theories (gressa theory and SQRF theory in particular) aren't even fully compatible, and yet I used
both of those in the last two parts of this analysis. That being said, a perfectly complete analysis of a universe as rich in possibilities as
Lartravera would never be finished, and I'd say I've done a pretty thorough job with my analysis as is. When I began looking into Lartravera,
I only did so because the potential use of squared versions of the SI base units there interested me, and when I returned to study Lartravera further,
I originally only did it with the purpose of analyzing how other units of measurement apply to it. Over time, it became clear that Lartravera had
much more to analyze than the units used to measure it, and I began to branch out in Chapter 3 but only fully got into looking at non-unit-based parts
of Lartravera starting in Chapters 5 and 6. Now I've written nine chapters, the latter ones being much longer than the early ones, and at this point
I've said so much about Lartravera that I've just about run out of topics to discuss about it without going into too much unnecessary detail.
There's always more to say about this fascinating universe and the differences between it and our own universe,
and perhaps someday I will have more to say... but for now, my analysis of Lartravera is complete.
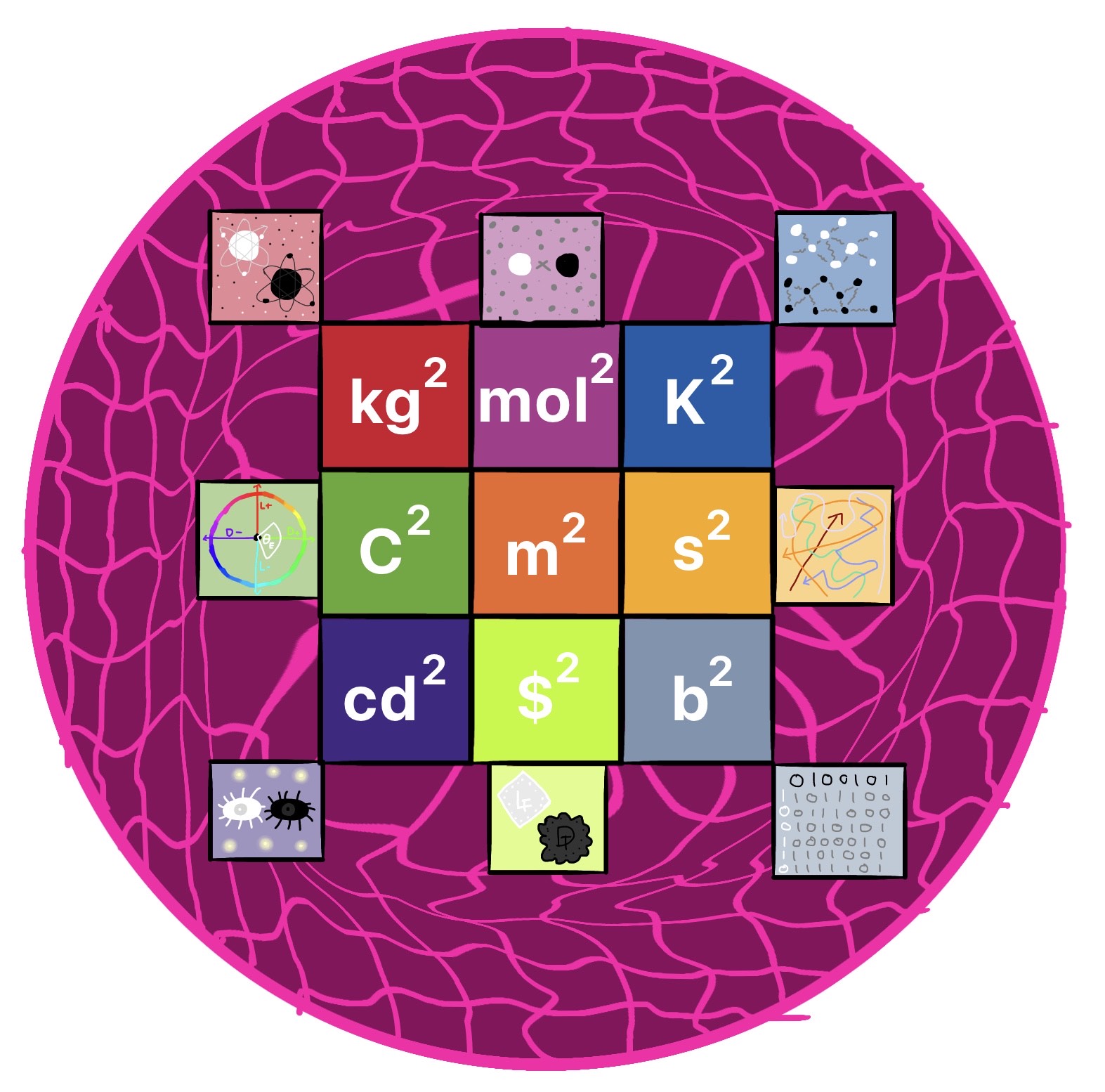
 Chapter 1: Intro to Lartravera
Chapter 1: Intro to Lartravera Chapter 2: Mechanical Units
Chapter 2: Mechanical Units Chapter 3: Atoms and Molecules
Chapter 3: Atoms and Molecules
 Chapter 4: Electrical Units
Chapter 4: Electrical Units Chapter 5: Streggis and Temperature
Chapter 5: Streggis and Temperature Chapter 6: Consciousness and Time
Chapter 6: Consciousness and Time Chapter 7: Reality Fluctuations
Chapter 7: Reality Fluctuations Chapter 8: Light and Energy
Chapter 8: Light and Energy Chapter 9: The Lartraveran Cosmos
Chapter 9: The Lartraveran Cosmos Conclusion
Conclusion