The DIVE Color Scheme

An explanation of the appearances of tiles in one of 2048's most unique variants

A finished game of DIVE

You've probably heard of 2048, the internet game from 2014 where you move numbered tiles around on a grid, with two equal tiles merging into a tile twice as large upon colliding. 2048 inspired thousands of variants; most of them were simple visual changes, but others were more substantial, such as three equal tiles merging instead of two, tiles that follow the Fibonacci sequence instead of the powers of two, 3D and 4D boards, hexagonal board, a version where some tiles decay away if left around too long, a version with tiles that could represent any one of multiple options, a version where any amount of equal tiles can merge, and so on.

Out of these many variants, one stands out to me as the most interesting of the bunch: DIVE, a variant by Alex Fink that was also made in 2014. DIVE has two fundamental differences from 2048. The first one is the merge rule: whereas 2048 only allows two tiles to merge if they're equal, DIVE allows two tiles to merge as long as one of them is a multiple of the other one (equivalently, if one of them is a factor of the other one). If the only spawning tile was 2 like in 2048, then the game would never end - every new tile would be even, so you could keep merging 2s with them forever! As such, the second difference is in the spawning tiles. DIVE has three options for how its tile spawns work: in the first the possible spawns are 2, 3, 5, and 7, but in the other two the list of spawning tiles updates dynamically: whenever a new tile is made, if it has any factors that aren't accounted for by the existing spawning tiles, that remaining factor is unlocked as a new spawning tile. For example, if you merge 4+2=6 and your only spawning tile is 2, then 3 is unlocked as a new spawning tile. In the second option seeds are permanent, but in the third option (which is the default, and the most fun way to play DIVE), seeds can be removed from the list if no multiples of them remain on the board.

These two differences completely change how DIVE is played, making it a much more dynamic game, with a lot of different paths of tiles a single run could go down! DIVE is an example of emergent gameplay, where the game becomes complex not because its rules are inherently complicated, but because they interact in neat ways; in DIVE's case, the emergent gameplay comes from the strategies that arise not because of any intent from the developer, but because the mathematics behind the game guides the strategy in that direction. There's a lot I could say on this, but DIVE's strategy is not what this post is here to discuss. Besides, I'm no expert - my high score is (at the time of writing) 65,884, in a game where the world record is (at the time of writing) over 5 million. Granted, DIVE scores can grow exponentially, so I'd still say I'm good at the game, but if you want to learn DIVE's strategy, this blog post from the game's world record holder has plenty to say about that.

What I'm here to discuss today is DIVE's most interesting non-gameplay feature: the color schemes of the tiles. In 2048, each tile is twice as large as the last, so the colors of the tiles can be preset for each tile number in the game, since at maximum there are only seventeen types of tile you could possibly encounter. But in DIVE, every integer above 1 can hypothetically be reached as a tile! This means that there has to be some procedural way to generate tiles based on their numbers, and indeed there is. But how does it work? Having recreated DIVE, including its color scheme, in my own catalog of 2048 variants, The 2048 Power Compendium, I've learned enough about it to answer that question and explain its system. I'll be sticking to the original DIVE's tiles for the most part, but the Compendium's version of the color scheme has a few differences that I'll be pointing out later on. Let's get started!

Tile Colors

The way a tile looks is based on the prime factorization of that number. In short, a prime number is a positive integer whose only factors are 1 and itself, and any number has exactly one way to write it as a product of primes (if you don't care about order, since multiplication is commutative): for example, 60's prime factorization is 2×2×3×5. Since DIVE's merges are about divisibility, having tiles be displayed based on their prime factorizations makes it easy to tell what tiles are divisible by each other.

The first three prime numbers are 2, 3, and 5, so those three primes determine the color of the tile. 2 is a dark red, 3 is a dark green, and 5 is a dark blue:

Numbers that are multiples of 2, 3, and/or 5 mix these colors. 6 is red and green mixed (which makes a muddy olive color), 10 is red and blue mixed (which makes purple), and 15 is green and blue mixed (which makes cyan/teal):

Hey, wait a minute!

Yes?

2, 3, and 5 are the RGB primary colors, and those are the results of mixing those colors in RYB, not RGB! Red and green are supposed to make yellow, and red and blue are supposed to make magenta! Where are my yellows and magentas?!

OK, I may have fibbed a bit there. RGB is indeed the color system used, but the distribution of the colors is not even. Because 3 is bigger than 2, each factor of 3 adds more green than each factor of 2 adds red, and likewise factors of 5 add more blue than the others add of their respective colors. As such, 6, with one each of 2 and 3, is more green than red, and likewise for the others. The amounts of each color added by each factor are lined up so that they each reach full brightness at approximately equal sizes: the powers of 2 reach full red at 128, the powers of 3 reach full green at 81, and the powers of 5 reach full green at 125. To be specific, here's the amount of each color at each power of these primes, where 0 is no color and 255 is full brightness:

Powers of 2: 2 has 68 red, 4 has 136 red, 8 has 170 red, 16 has 204 red, 32 has 221 red, 64 has 238 red, 128 has 255 red

Powers of 3: 3 has 102 green, 9 has 170 green, 27 has 221 green, 81 has 255 green

Powers of 5: 5 has 136 blue, 25 has 204 blue, 125 has 255 blue

So, while 6 isn't yellow, larger powers of 6 (and indeed larger "3-smooth" numbers (numbers whose prime factorizations contain no primes larger than 3) in general) get closer to yellow, as the powers of 2 and 3 involved get closer to 255 red and 255 green respectively. If a tile has more factors of a prime than is needed to reach full brightness of that color, it just stays at full brightness of that color. This means that not every tile is unique: 128 and 256 look the same, for instance, and indeed any multiple of 256 looks the same as the tile that's half of it (and any multiple of 243 looks the same as the tile that's a third of it, and any multiple of 625 looks the same as the tile that's a fifth of it). Here's a grid showing all the possible plain colors that a tile can be:

The original DIVE doesn't allow changing the grid size, so I used the Power Compendium version to make this arrangement.

Prime Patterns

The human eye sees color three-dimensionally, as it has three light receptors: one for reddish wavelengths, one for greenish wavelengths, and one for bluish wavelengths. So far as DIVE is concerned, this means that "5-smooth" numbers (numbers whose prime factorizations contain no primes larger than 5) already cross the full range of colors we can see (not every possible color, of course, since the amounts of each primary increase in discrete steps, but you get my point), so we're going to need some other method to handle primes larger than 5.

Each prime larger than 5 gets its own pattern that is placed on top of the tile's background color. This pattern will be half-transparent if only one factor of that prime is in the number, but if it has at least two factors of that prime (i.e. it's a multiple of the prime's square), then the pattern will be at full opacity.

The first three non-color primes get special patterns: 7 uses a black and white conic gradient, 11 is black and white circles, and 13 is black and white stripes:

These patterns may be combined, both with colors and with other patterns. Here are some examples:

The first six primes may have gotten specifically chosen colors and patterns, but if we want a pattern for every prime, eventually we need to start procedurally generating these too. After 13, the prime patterns are stripes in various colors, sometimes multiple colors. Here are the first few:

The colors on these stripes aren't random: there's an algorithm that decides what colors the stripes are for any given prime. How does this algorithm work?

Generating Prime Stripes

The basic loop of the algorithm is as follows: take the prime, add 1 then divide by 2, factor out any factors of 2, 3, 5, or 7, and repeat. This generates a set of "residues" that are used to determine the colors of each "layer" of the stripe.

Let's begin with the simplest case, where there's only one residue. This results in a single-layered stripe. The factors of 2, 3, and 5 factored out determine the color of a stripe layer. With 17, when you add 1 then divide by 2, you get 9, and 9 is 3² so it's green, thus the stripes for 17 are green. With 19, when you add 1 then divide by 2, you get 10, and the 10 tile is purple, thus the stripes for 19 are purple.

You may have noticed that the stripes are full-brightness green and purple rather than the darker green and purple of the actual 9 and 10 tiles: the colors of stripes take the colors of that residue and then brighten them exactly enough so that their most prominent prime color (i.e. whichever of red, green, or blue they have the most of) is set to 255, with the other two being multiplied by the same ratio. As such, stripes can contain non-greyscale colors lighter than a "color wheel" color (a color without any black or white in it, which in RGB means one of the three values is 255, another is 0, and there's no restriction on the third), but not ones darker than a color wheel color.

There's another significant difference between the stripe colors and the tile colors. 23's residue is 12, but 23's stripes are a more rich orange than 12's golden orange:

23² used instead of 23 to make the stripes more clear. 23²×12 on the right is there to show that the colors don't blend into each other.

The culprit here is that, to give the stripes more color variety, the greens are weaker in the stripes than they are in the tiles: instead of 102, 170, 221, 255, the sequence of green amounts for the amount of factors of 3 in a stripe residue is 68, 136, 204, 255.

When there are any factors of 7 in the residue, the stripes gain a gradient effect that goes between the residue color, white, the residue color, black, and repeat. 41 and 83 are examples of this:

41, 83, and their squares for clarity.

41's residue is 21, which is 3×7, so it's green with the "7 in stripe" gradient effect. Likewise, 83's residue is 42, which is 6×7, 6 with the weakened greens is yellow instead of chartreuse/olive, so it's yellow with the "7 in stripe" gradient effect.

OK, that explains the single-color stripes. What about the two-part stripes? Aren't there more of those than there are single stripes eventually?

Let's use 43 as an example to explain how those work:

43² used instead of 43 - again, it's easier to analyze them when they're at full opacity.

When you take 43 and add 1 then divide by 2, you get 22. 22 is 2×11, but a stripe layer can only contain factors of 2, 3, 5, and 7. As such, the 2 is factored out of 22 and becomes the red in the outer layer of the stripe. The remaining 11 is increased by 1 then divided by 2 a second time, giving us a "super-residue" of 6 (I like to call the residue of a residue the "second residue", but they're called "superresidues" in the code, so I'll use both terms here), which becomes the yellow in the inner layer of the stripe.

Here's some more examples:

37's residue (add 1 then divide by 2) is 19, which has no factors of 2, 3, 5, or 7, so the first stripe layer is 1's black, then the superresidue is 10, so 37's stripes are black outside, purple inside. (Oh, and here's confirmation that the outer stripes are indeed black rather than transparent: )

137's residue is 69, which is 3×23, so the 3 is factored out to become the outer green. 23's residue is 12, so the inner stripe is orange.

131's residue is 66, which is 2×3×11. Both the 2 and the 3 are factored out, so the first stripe layer is 6's yellow. The remaining 11's residue is... 6 again, so the inner stripe is also yellow. To ensure that stripes where both layers are the same color don't look like single-color stripes, when a stripe has multiple layers, the inner layers have more opacity then the outer layers.

103's residue is 52, which is 2×2×13. Both 2's are factored out, so the outer stripe's number is 4, which is red - because of the "brighten the stripes so one of the three RGB values is 255" rule, all powers of 2 will show up as the same red in a stripe (and likewise for powers of 3 and powers of 5). The remainder is 13, whose residue is 7, thus the inner stripe is 1's black with the 7 gradient effect.

I think that's enough examples, but there's a few more rules to keep in mind.

Larger primes have their stripes be thinner and packed more closely together - to be specific, they get thinner at a rate based on the square root of the prime in question, so a prime that's around four times larger than another would have stripes around twice as dense. This is to ensure that primes like 31 and 127, whose stripes are both pure red, are distinct. Similarly, how short the inner stripes are (and thus how often they repeat) is based on the square root of the second residue (the "superresidue"):

The stripes get thinner since the primes are getting larger, but the second residue is 6 for all these primes, so the lengths of the inner stripes are the same...

...whereas here, the second residues are also increasing (10, 16, 40), so the inner stripes are getting more packed together too.

The direction the stripes are in also isn't random - the formula involves the index of the prime (17 is the 7th prime, 19 is the 8th prime, etc.) and the golden ratio (the golden ratio is by some definitions the "most irrational" number, so using it makes it as unlikely as possible for stripes' directions to overlap completely) - but it's not particularly important, it's supposed to "feel" random and so it may as well be.

Also, you may have noticed that single-layer stripes fade to black on their edges - this is to ensure that they don't become invisible on a tile of the same color as them. Stripes with multiple layers do not have this fade, since in most circumstances the layers will be different colors and thus the layers can't all be hidden at once (although this isn't foolproof...).

Special Cases

and the differences between the original and the Power Compendium

You should now have a good idea of how most of the primes' stripes are generated, but there's still some special cases to go over. This is also where my implementation of this scheme in the 2048 Power Compendium starts to differ from the original version in a few ways - I'll explain those differences as we go. As such, I'll be comparing the tiles in the two versions: the original will be on the left, the Power Compendium version will be on the right. I'll go in ascending order of the primes I'm examining for these.

I claimed earlier that 13 was a special pattern like 7 and 11 are, but that was another fib. 13 is actually the first stripes prime: 13's residue is 7, so the stripes are black with the 7 gradient effect. But 13 sure looks like it's special like 7 and 11 are at a glance, and in the Compendium it actually is hardcoded like 7 and 11 are, because I didn't like the very slight slant 13 had and wanted to make it perfectly vertical.

I didn't want there to be stripes that were mostly black, so when the outermost stripe color is 1 (or any other purely greyscale color), the Compendium brightens it halfway closer to white (so 1's black becomes exactly medium grey). This does not happen on inner stripes, only the outermost one.

There's nothing particularly special about 41, but this is a good time to discuss two minor differences.

The script that the original DIVE used to generate the images was in Python, in which there are more options for gradient interpolation, allowing the gradients in this case to be more "blurry" and thus feel more smooth. But whereas DIVE made those stripes in Python and saved them as images to recall during gameplay, the Power Compendium version of DIVE generates the stripes on the fly using CSS, which means its gradients have to use linear interpolation (CSS does not, so far as I know, have gradient interpolation options) - so if the gradients look slightly "rougher" in the Compendium's version of the DIVE scheme, that's why.

The other, more obvious thing to note is the difference in brightness here. In addition to the "half opacity with one factor, full opacity with two" rule, in the original DIVE even the full-opacity textures are still at least a bit transparent, with some primes being more transparent than others (I'm not sure what the rules are about this, although stripes with factors of 7 in them seem especially transparent to me). This, in my opinion, makes many textures too dim to see, so the Compendium doesn't do this - in the Compendium version, half-opacity is 50% opacity and full-opacity is 100% opacity, period.

So far we've only seen stripes with one or two layers, but it's possible for them to have more than that - these two primes are examples of primes with three-layered stripes. 73's residue is 37, 37's residue is 19, and 19's residue is 10 (this would be a "third residue" or "supersuperresidue"), so 73's stripes are two black layers then a purple layer. 257's residue is 129, factor out the 3 (green), 43's residue is 22, factor out the 2 (red), 11's residue is 6 (yellow), so 257's stripe layers are green, red, yellow. In the original DIVE, when a stripe has three layers, it's actually the second layer, not the third, that's furthest on the inside - the third layer is the middle instead. In the Compendium version, the third layer is the innermost layer. The original DIVE probably went the way it did to make 73 more distinct from 37 - since both 1's would be black, 73 would just be "37 but the purple is thinner" (when it's on its own rather than on a non-black tile, that is) if the third layer was the innermost, whereas having the second layer be the innermost instead gives us black-purple-black as seen above. The Compendium gets around this issue, since the outermost 1 is grey but the middle 1 isn't. The reason I reverted this choice for the Compendium version will be discussed later.

97's residue is 49, which is 7². In the original DIVE, the 7 stripe gradient is unaffected by there being multiple factors of 7, but in the Compendium version the gradient is denser the more factors of 7 there are.

The one significant part of the original DIVE's stripe rules I don't understand is what happens when the outer layer of a multi-layer stripe has a factor of 7 in it. 181's residue is 91, which is 7×13, so the outer stripe is 7, and then 13's residue is 7 so the inner stripe is also 7. 307, meanwhile, has a residue of 154, 2×7×11, so the outer stripe is 14 and the inner stripe is 11's residue, i.e. 6. What I think the original DIVE is doing is somehow making the gradient's color fade in at the outside of the stripes, so 181's stripes get darker towards their edges since 7's gradient color is 1's black, and 307's stripes get redder towards their edges since 14's gradient color is 2's red. Since I didn't know how to handle this, the Compendium goes for a different approach, simply giving the outer stripes a gradient like how the inner stripes get a gradient if they're a multiple of 7.

241's residue is 121 (11²), and 337's residue is 169 (13²). When a residue is a power of a prime greater than 7, the original DIVE responds by making the inner stripe's color be based on the residue of that prime rather than the power of the prime, but its opacity is doubled, hence why 241 gets a bright yellow (the color associated with 11's residue) even with only one factor of the prime. The Compendium, on the other hand, retains its "half opacity is half opacity, full opacity is full opacity" rule, so instead of doubling the opacity it doubles the inner stripe density, i.e. the color is still 11's residue's color but the inner stripes are bunched together at the density expected for 121 instead of 11.

These prime patterns could in theory continue forever. Let's look at a decently large example: 409. 409's residue is 205, which is 5×41. Factoring out the 5 gives us blue outer stripes. 41's residue is 21, so the inner stripes are 3's green with the 7 gradient, giving us this stripe pattern:

Uh, why is this tile blank?

OK, there's one more snag to all this - eventually the primes get too big.

The Limits of the Stripes

and how the Power Compendium surpasses them

As I mentioned previously, the original DIVE has all of the prime images saved as image files. This means that there has to be a limit, some final pattern after which the stripes stop. As we saw previously, 409 is past this limit, so in the original DIVE it doesn't get a texture at all. But having primes without any texture makes it so at numbers this big, the goal of the DIVE color scheme, to make it easy to tell what tiles can merge, is dampened: two different primes without a texture will both be plain black tiles, but they can't merge. The Power Compendium, since it generates its stripes on the fly via CSS, doesn't have to have this limit, and indeed primes like 409 get their expected textures there:

But where is the limit of the original DIVE? It turns out to be at 373. 373's residue is 187, which is 11×17. We discussed previously that DIVE has a method for handling primes whose residue is a power of another prime, but now we have a prime whose residue is a product of two different primes. The original DIVE's stripe generation algorithm does not have a way to handle this, so it crashes here. As such, 367 is the last prime to get a texture in the original DIVE: 373 doesn't get one, and neither does any prime above 373, even though there are plenty of primes that the algorithm could generate stripes for beyond 373 - since 373 doesn't work, it just stops there.

So what does the Power Compendium do for 373? Here it is:

The 11 and 17 are separated and each have their residue taken, giving us the yellow from 11's residue of 6 and the green from 17's residue of 9, and the inner stripes alternate between these two types. Since 17 is bigger than 11, the 17 inner stripes are longer than the 11 inner stripes. To see why I included the length difference, here's a larger example:

Square included for clarity, since the stripes are hard to see on the original.

2161's residue is 1081, which is 23×47. 23 and 47's residues, 12 and 24, are similar colors, so the length difference helps in telling them apart. This isn't strictly necessary here, but if the primes in the product were, say, 31 and 127, then they'd be the exact same color, so the length difference would be required, otherwise you wouldn't be able to tell it was a "two inner stripe types" pattern.

The other case where the original DIVE's stripe algorithm would fail is when there are more than three layers. The Compendium's version, on the other hand, does have support for stripes with more than three layers (this is why I had to make the third layer be the innermost when there are three layers, because the way the original DIVE does it doesn't generalize well to arbitrarily many layers). The earliest example of this I could find is 1021, and it's not the best example (so if someone finds a better one, let me know!):

Stripe layers here are 7, 1, 1, 10, so gradient on the outside, two layers of black, purple on the inside.

So, with both of the remaining issues taken care of, does that mean that the Power Compendium's version of the DIVE color scheme can keep generating patterns forever? Well... in theory it can, but there are two issues. First, eventually the stripes would get so dense that you couldn't see them as anything more than a mesh anymore. Here's what a prime in the low five-digit range and a prime in the low six-digit range would look like:

Don't see anything in the latter? Let's square that:

As you can see, the stripes are so dense that you can't really tell them apart anymore, they all blend together. But even if we were to slow down the stripe density, or do something else to avoid this issue, there's another problem: prime factorization is hard. The most common way to check whether a number is prime is to check every prime up to the square root of that number to see if any of them divide it, and if not, it's prime. When we're working with numbers in the millions and billions, this means generating and checking thousands of primes. Maybe a computer can pull that off, but if you're working with numbers in the trillions or more, now you're checking millions of primes, which will take too long even for computers. Prime factorization being hard is something that computers rely on, in fact: most algorithms for cryptography (encryption, keeping messages secure) rely on using huge primes (hundreds or even thousands of digits) as part of their algorithms. If numbers made from multiplying those primes could easily be factored, the messages wouldn't be securely encrypted.

My point here is that we can't expect to factor numbers of any size, at some point there has to be a limit to the amount of prime factors we check. The Compendium, somewhat arbitrarily, chooses this limit to be 1,000, so the last prime checked is 997. But it has one more trick up its sleeve:

3×1009, using an "inner tile" for the post-1000 prime

If, after dividing out every factor from 2 to 997, what remains is larger than 1, then that leftover number is subtracted by 1 and displayed as an "inner tile" within the tile. For example, 3027 is 3 times 1009. The 3 becomes the green on the outside, then 1009 has no prime factors below 1000 in it, so it becomes an inner tile. 1009 minus 1 is 1008, so the 1008 tile is the inner tile used. It's possible for there to be multiple layers of inner tile:

2027 has no prime factors below 1000, so 2026 is the inner tile, but 2026 itself has a prime factor above 1000, that being 1013, thus the second layer of tile is the 2 factored out from 2026, and 1012 (1013 minus 1) is used as a second layer of inner tile. Thankfully, the amount of layers can't spiral too far out of control: since any number that needs an inner tile must be odd, and 1 is subtracted to make the inner tile, the inner tile must always be even, so at each layer at least a 2 will be divided out. As such, the amount of layers cannot grow any faster than the base-2 logarithm of the tile, and usually there are significantly less layers than that. (If you're wondering why 1021 and 2161 got patterns earlier, let me clarify: they use inner tiles in the actual game, the patterns I showed earlier are what they would look like if the patterns did go that far.)

The inner tiles approach breathes additional life into the goal of DIVE's color scheme. As long as the tile is under a million, if it has any prime factors greater than 1,000, it can't have more than one, which means the inner tile must be prime. As such, despite only checking for primes up to 1,000, the ability to distinguish primes on the tiles goes up to tiles of size one million, although past that prime factors greater than 1,000 will blend together:

The tile on the right is the product of the left two, but isn't visually connected to them.

Since the game isn't checking for prime factors above 997, it doesn't know that 1,028,171 is the product of 1,009 and 1,019, so it's just treated as its own "prime" for the sake of the inner tile. Still, for a game where (as of writing) only one known player has ever scored over a million, and the original version of the color scheme lost consistency at 373, getting up to a million is pretty good, don't you think? Besides, I find it very unlikely that the visual inconsistency above a million would be relevant. Even if you did stumble into a number with multiple prime factors above 1,000 in DIVE, I suspect you'd be more likely to find it as its own seed than you would be to actually get up to it from one of its factors.

Conclusion

And that's the color scheme that DIVE, and the 2048 Power Compendium version of it, use to display their tiles. DIVE is one of my favorite games, and the color scheme was what originally got me hooked on it - and I'd say it does its job of making it easy to tell what tiles are multiples of each other, and thus what tiles can merge, quite well.

...oh, and if you're wondering about that crazy jumble of colors that the score starts out as...

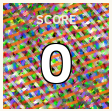
...0 is a multiple of every prime, so it has all of the textures at once. (For the sake of consistency, the Power Compendium version of DIVE's 0 stops at 367's texture even though the Compendium's textures go further than that)

Want to see this color scheme in action? Then go play DIVE or its implementation in The 2048 Power Compendium... or use the tile generator below to see what tiles of various numbers look like! (disclaimer: the text size isn't necessarily accurate, but the color and stripes should be)

Number: